Zadanie - zbieżność szeregu geometrycznego
Treść zadania:
Dla jakich wartości parametru \(x\) szereg geometryczny \(1+x^3+x+1+(x^3+x+1)^2+(x^3+x+1)^3+...\) jest zbieżny?
Rozwiązanie zadania
Szereg geometryczny ma postać:
Mamy więc:
\(1+x^3+x+1+(x^3+x+1)^2+(x^3+x+1)^3+...\)
\(a_1=1\)
\(q=x^3+x+1\)
Warunkiem zbieżności szeregu geometrycznego jest \(|q|=<1\), czyli \(-1<q<1\).
Mamy więc do rozwiązanie dwie nierówności:
\(1)\ \ q<1\)
\(x^3+x+1<1\)
\(x^3+x+1-1<0\)
\(x^3+x<0\)
\(x(x^2+1)<0\)
Ponieważ \(x^2+1\) jest zawsze dodatnie, to powyższy iloczyn jest ujemny, jeśli \(x<0\), co stanowi rozwiązanie powyższej nierówności.
\(x<0\)
Rozwiązujemy teraz drugą nierówność:
\(2) \ q>-1\)
\(x^3+x+1>-1\)
\(x^3+x+1+1>0\)
\(x^3+x+2>0\)
Otrzymaliśmy nierówność algebraiczną. Wielomian po lewej stronie nierówności, oznaczmy go przez \(W(x)\), musimy rozłożyć na czynniki. Szukamy pierwiastków wielomianu wśród podzielników wyrazu wolnego, a więc pośród liczb: \(1, -1, 2, -2\).
\(W(x)=x^3+x+2\)
\(W(1)=1^3+1+2=4\neq 0\)
\(W(-1)=(-1)^2-1+2=0\)
\(W(2)=8+2+2=12\neq 0\)
\(W(-2)=-8-2+2=-8\neq 0\)
Liczba \(-1\) jest pierwiastkiem wielomianu \(W(x)\). Dzielimy więc wielomian \(W(x)\) przez \(x-x_1=x+1\).
Nasza nierówność zatem przyjmuje postać:
\(x^3+x+2>0\)
\((x+1)\underline{(x^2-x+2)}>0\)
\(a=1,\ b=-1,\ c=2\)
\(\Delta=b^2-4ac=(-1)^2-4\cdot 1\cdot 2=1-8=-7<0\)
Wyróżnik trójmianu kwadratowego, który występuje w powyższej nierówności algebraicznej jest ujemny, oznacza to, że trójmian nie ma pierwiastków. Ponieważ współczynnik \(a\) tego trójmianu jest dodatni, ramiona paraboli skierowane są do góry, parabola nie przecina osi \(OX\), więc wszystkie wartości trójmianu kwadratowego są dodatnie (wyrażenie \(x^2-x+2\) jest dodatnie dla każdej wartości \(x\)). Powyższa nierówność jest zatem spełniona wtedy i tylko wtedy, gdy \(x+1>0\) (bo skoro jeden czynnik iloczynu jest dodatni i wynik iloczynu jest dodatni, to drugi czynnik iloczynu również musi być dodatni).
\(x+1>0\)
\(x>-1\)
Ponieważ obie rozpatrywane nierówności muszą być spełnione jednocześnie, rozwiązania zadania szukamy poprzez znalezienie części wspólnej obu wyznaczonych zbiorów rozwiązań:
\(\begin{cases} x>-1 \\ x<0 \end{cases}\)
Odpowiedź
© medianauka.pl, 2010-01-01, ZAD-477
Zadania podobne
Zadanie nr 3.
Zamienić liczbę 0,(c) na ułamek zwykły, gdzie \(c\in \lbrace 1,2,3,4,5,6,7,8,9\rbrace\).
Zadanie nr 4.
Środki kwadratu o boku długości a połączono ze sobą. W ten sposób został utworzony kwadrat, którego środki boków znów połączono ze sobą i tak dalej. Obliczyć pole powierzchni wszystkich utworzonych w ten sposób figur geometrycznych.
Zadanie nr 5.
Nieskończenie wiele odcinków, każdy o długości stanowiącej 1/3 długości poprzedniego, ustawiono w linii prostej jeden za drugim. Jakiej długości linijki trzeba dysponować, aby zmierzyć ich łączną długość, jeżeli najdłuższy odcinek ma długość 5 cm?
Zadanie nr 7.
Obliczyć \(1-\frac{1}{\sqrt{2}}+\frac{1}{2}-\frac{1}{2\sqrt{2}}+...\).
Zadanie nr 8.
Rozwiązać równanie \(5+\frac{5}{x}+\frac{5}{x^2}+\frac{5}{x^3}+...=10\).
Zadanie nr 10 — maturalne.
Określamy kwadraty \(K_1, K_2, K_3, ...\) następująco:
• \(K_1\) jest kwadratem o boku długości \(a\).
• \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1:3\).
• \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1:3\).
i ogólnie, dla każdej liczby naturalnej \(n\geq 2\)
• \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_n-1\) i dzieli ten bok w stosunku \(1:3\).
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
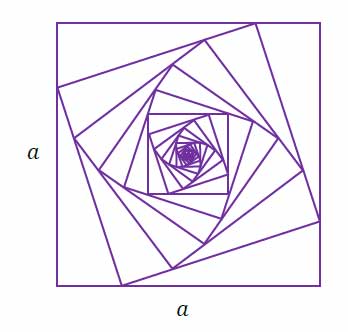
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu. Zapisz obliczenia.