Szereg geometryczny
Jeżeli dany jest ciąg geometryczny \((a_n)\) o ilorazie \(q\), to możemy utworzyć nowy ciąg \(S_n\) w następujący sposób:
\(S_1=a_1\)
\(S_2=a_1+a_2\)
\(S_3=a_1+a_2+a_3\)
\(S_4=a_1+a_2+a_3+a_4\)
\(...\)
\(S_n=a_1+a_2+a_3+...+a_n\)
\(...\)
Widzimy, że n-ty wyraz stanowi sumę \(n\) kolejnych wyrazów ciągu \((a_n)\), począwszy od wyrazu pierwszego.
Ciąg \((S_n)\) nazywamy szeregiem geometrycznym lub ciągiem sum częściowych ciągu geometrycznego.
Szereg geometryczny — wzór
Ponieważ n-ty wyraz ciągu geometrycznego wyraża się wzorem \(a_n=a_1\cdot{q^{n-1}}\), to szereg geometryczny będzie miał następującą postać:
Przeanalizujemy powyższe określenie szeregu geometrycznego na przykładzie.
Przykład
Dane jest koło o promieniu \(r\). Rozcinamy je na dwie części o równych polach \(p\), a następnie jedną z tych części znów na połowę itd.
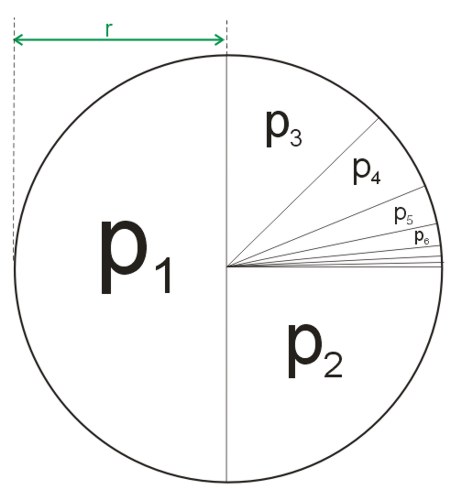
Pole koła wyraża się wzorem \(p=\pi{r^2}\). Każda z części ma pole o połowę mniejszą niż większa część. Obliczmy więc pola poszczególnych części figury.
\(p_1=\frac{\pi r^2}{2}\)
\(p_2=\frac{\pi r^2}{4}=p_1\cdot \frac{1}{2}\)
\(p_3=\frac{\pi r^2}{8}=p_2\cdot \frac{1}{2}\)
\(p_4=\frac{\pi r^2}{16}=p_3\cdot \frac{1}{2}\)
\(...\)
\(p_n=\frac{\pi r^2}{2^n}=p_{(n-1)}\cdot \frac{1}{2}\)
\(...\)
Pola kolejnych figur tworzą ciąg geometryczny \((p_n)\) o ilorazie \(q=\frac{1}{2}\).
Utworzymy teraz szereg geometryczny. Dodajemy do siebie kolejne pola, tworząc sumy pośrednie:
\(s_1=p_1=\frac{\pi r^2}{2}\)
\(s_2=p_1+p_2=\frac{\pi r^2}{2}+\frac{\pi r^2}{4}=\frac{3\pi r^2}{4}\)
\(s_3=p_1+p_2+p_3=\frac{\pi r^2}{2}+\frac{\pi r^2}{4}+\frac{\pi r^2}{8}=\frac{7\pi r^2}{8}\)
\(s_4=p_1+p_2+p_3+p_4=\frac{\pi r^2}{2}+\frac{\pi r^2}{4}+\frac{\pi r^2}{8}+\frac{\pi r^2}{16}=\frac{15\pi r^2}{16}\)
\(...\)
\(s_n=p_1+p_2+p_3+...+p_n=\frac{\pi r^2}{2}+\frac{\pi r^2}{4}+\frac{\pi r^2}{8}+...+\frac{\pi r^2}{2^n}=\pi r^2[1-(\frac{1}{2})^n]\)
\(...\)
Jak obliczyliśmy \(s_n\)? Skorzystaliśmy ze wzoru na sumę \(n\) wyrazów ciągu geometrycznego.
\(s_n=a_1\frac{1-q^n}{1-q}=\frac{\pi{r^2}}{2}\cdot{\frac{1-(\frac{1}{2})^n}{1-\frac{1}{2}}}=\pi{r^2}[1-(\frac{1}{2})^n]\)
W taki oto sposób utworzyliśmy ciąg geometryczny.
Warto jeszcze zwrócić uwagę na to, że kolejne wyrazy ciągu geometrycznego coraz bardziej zbliżają się do wartości pola koła. Możemy to nawet policzyć, obliczając odpowiednią granicę:
\(\displaystyle\lim_{n\to\infty}S_n=\lim_{n\to\infty}[\pi{r^2}[1-(\frac{1}{2})^n]]=\lim_{n\to\infty}(\pi{r^2}-\pi{r^2}\frac{1}{2^n})=\pi{r^2}-0=\pi{r^2}\)
Zbieżność szeregu geometrycznego
Szereg zbieżny to taki szereg, który ma granicę. Szereg rozbieżny to taki, który nie jest zbieżny.
Szereg geometryczny jest zbieżny, gdy \(|q|<1\) i jest rozbieżny, gdy \(|q|\geq{1}\).
Suma szeregu geometrycznego
Szereg geometryczny jest zbieżny , gdy \(|q|<1\) i ma sumę:
Szereg geometryczny jest rozbieżny, gdy \(|q|\geq{1}\).
Powyższe oznacza, że jeżeli \(-1<q<1\), to istnieje skończona suma szeregu geometrycznego.
Zastosowania szeregów geometrycznych
Dzięki wiedzy na temat szeregu geometrycznego możemy obliczać pola powierzchni różnych figur, długości nieskończonej liczby odcinków, objętości nieskończonej liczby brył, jeżeli spełnione są tylko pewne warunki. Czasem okazuje się, że wartości te wcale nie są nieskończone! Wyżej zastosowaliśmy szereg geometryczny dla koła.
Oto inny przykład.
Przykład 1
W środku koła o promieniu \(r\) rysujemy koło o promieniu o połowę krótszym. W środku tego małego koła rysujemy koło również o promieniu o połowę krótszym i tak dalej. Obliczyć pole powierzchni wszystkich kół.
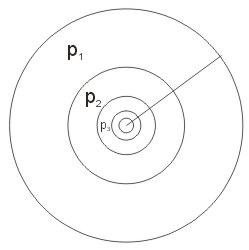 Na podstawie warunków zadania sporządzamy rysunek. Mamy do czynienia z nieskończoną liczbą kół, a naszym zadaniem jest obliczyć pole wszystkich tych figur.
Na podstawie warunków zadania sporządzamy rysunek. Mamy do czynienia z nieskończoną liczbą kół, a naszym zadaniem jest obliczyć pole wszystkich tych figur.
Wypiszmy pola poszczególnych figur:
\(p_1=\pi{r^2}\)
\(p_2=\pi{(\frac{r}{2})^2}=\pi{r^2}\cdot{\frac{1}{4}}\)
\(p_3=\pi{(\frac{r}{4})^2}=\pi{r^2}\cdot{(\frac{1}{4})^2}\)
\(p_4=\pi(\frac{r}{8})^2=\pi{r^2}\cdot(\frac{1}{4})^3\)
\(...\)
\(p_n=\pi{r^2}\cdot(\frac{1}{4})^{(n-1)}\)
Zatem pole wszystkich kół jest równe \(P=p_1+p_2+p_3+...\). Mamy więc do czynienia z szeregiem geometrycznym, wartość \(a_1=\pi{r^2}\), iloraz \(q=\frac{1}{4}\), a więc spełniony jest warunek zbieżności szeregu geometrycznego. Możemy obliczyć sumę, a więc pole wszystkich figur:
\(P=\frac{a_1}{1-q}=\frac{\pi{r^2}}{1-\frac{1}{4}}=\frac{4}{3}\pi{r^2}\)
Przykład 2
Zamienić liczbę \(0,(7)\) na ułamek zwykły.
Zauważamy, że:
\(0,(7)=0,777...= 0,7+0,07+0,007+0,0007+... = 0,7+0,7\cdot 0,1+0,7\cdot (0,1)^2+0,7\cdot (0,1)^3+...\)
Otrzymaliśmy więc szereg geometryczny o ilorazie \(q=0,1\) i \(a_1=0,7\). Sumując wszystkie wyrazy szeregu, otrzymujemy:
\(S=\frac{a_1}{1-q}=\frac{0,7}{1-0,1}=\frac{\frac{7}{10}}{\frac{9}{10}}=\frac{7}{9}\)
Pytania
Skąd się wziął wzór na sumę szeregu geometrycznego?
Ogólny wyraz szeregu geometrycznego to \(S_n=a_1\cdot{\frac{1-q^n}{1-q}}\). Zatem suma szeregu geometrycznego to granica:
\(\displaystyle S=\lim_{n\to\infty}S_n=\lim_{n\to\infty}(a_1\cdot \frac{1-q^n}{1-q})=\lim_{n\to\infty}[\frac{a_1}{1-q}\cdot (1-q^n)]=\)
\(\displaystyle =\lim_{n\to\infty}(\frac{a_1}{1-q}-\frac{a_1}{1-q}q^n)=\frac{a_1}{1-q}-\frac{a_1}{1-q}\cdot{\lim_{n\to\infty}(q^n)}=\frac{a_1}{1-q}-0=\frac{a_1}{1-q}\)
Założyliśmy tutaj, że \(|q|<1\), gdyż tylko wtedy \(\displaystyle \lim_{n\to\infty}q^n=0\). W przeciwnym przypadku granica ta jest nieskończona (niewłaściwa) i suma szeregu również jest nieskończona.
Szereg geometryczny a ciąg geometryczny. Czym się różni ciąg geometryczny od szeregu geometrycznego?
Ciąg to występujące po sobie pewne liczby. Szereg albo ciąg sum częściowych to suma kolejnych wyrazów ciągu. Każdy uporządkowany nieskończony ciąg \((a_1, a_2, a_3, ..., a_n)\) ma odpowiadający mu szereg \((a_1+a_2+a_3+…)\). Mówiąc inaczej szereg geometryczny to nieskończona suma, a jego wyrazy tworzą ciąg. Oto przykład:
- \(2,4,16,...\) — ciąg,
- \(2+4+16+...\) — szereg.
Zadania z rozwiązaniami

Zadanie nr 3.
Zamienić liczbę 0,(c) na ułamek zwykły, gdzie \(c\in \lbrace 1,2,3,4,5,6,7,8,9\rbrace\).

Zadanie nr 4.
Środki kwadratu o boku długości a połączono ze sobą. W ten sposób został utworzony kwadrat, którego środki boków znów połączono ze sobą i tak dalej. Obliczyć pole powierzchni wszystkich utworzonych w ten sposób figur geometrycznych.

Zadanie nr 5.
Nieskończenie wiele odcinków, każdy o długości stanowiącej 1/3 długości poprzedniego, ustawiono w linii prostej jeden za drugim. Jakiej długości linijką trzeba dysponować, aby zmierzyć ich łączną długość. Najdłuższy odcinek ma długość 5 cm?

Zadanie nr 7.
Obliczyć \(1-\frac{1}{\sqrt{2}}+\frac{1}{2}-\frac{1}{2\sqrt{2}}+...\).

Zadanie nr 8.
Rozwiązać równanie \(5+\frac{5}{x}+\frac{5}{x^2}+\frac{5}{x^3}+...=10\).

Zadanie nr 10.
Dla jakich wartości parametru \(x\) szereg geometryczny \(1+x^3+x+1+(x^3+x+1)^2+(x^3+x+1)^3+...\) jest zbieżny?

Zadanie nr 11 — maturalne.
Określamy kwadraty \(K_1, K_2, K_3, ...\) następująco:
• \(K_1\) jest kwadratem o boku długości \(a\).
• \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1:3\).
• \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1:3\).
i ogólnie, dla każdej liczby naturalnej \(n\geq 2\)
• \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_n-1\) i dzieli ten bok w stosunku \(1:3\).
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
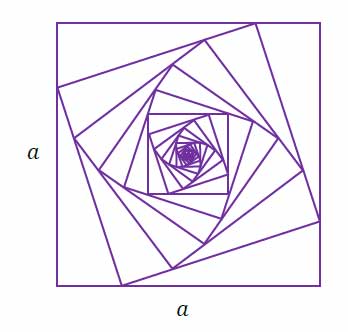
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu. Zapisz obliczenia.
Powiązane materiały
 Szereg geometryczny
Szereg geometryczny© medianauka.pl, 2009-09-06, A-314
Data aktualizacji artykułu: 2023-05-13

 Szereg geometryczny
Szereg geometryczny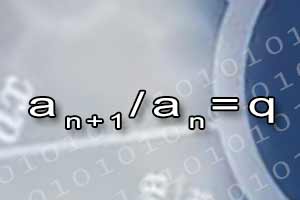 Ciąg geometryczny
Ciąg geometryczny Granica ciągu
Granica ciągu