
Zadanie maturalne nr 21, matura 2016 (poziom podstawowy)
Treść zadania:
W układzie współrzędnych dane są punkty \(A=(a,6)\) oraz \(B=(7,b)\). Środkiem odcinka \(AB\) jest punkt \(M=(3,4)\). Wynika stąd, że:
A. \(a=5\) i \(b=5\)
B. \(a=-1\) i \(b=2\)
C. \(a=4\) i \(b=10\)
D. \(a=-4\) i \(b=-2\)
 Rozwiązanie zadania
Rozwiązanie zadania
Jeżeli końce odcinka \(\overline{AB}\) mają współrzędne: \(A=(x_A,y_A),\ B=(x_B, y_B)\), to współrzędne środka odcinka obliczamy ze wzoru:
W naszym zadaniu dane są współrzędne środka odcinak \(M=(x_s,y_s)=(3,4)\). Mamy więc:
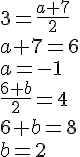
 Odpowiedź
Odpowiedź
© medianauka.pl, 2016-11-01, ZAD-3245


Zadania podobne
Zadanie nr 1.
Dane są punkty \(A=(-3,-2), B=(2, -2)\). Obliczyć długość odcinka \(\overline{AB}\).
Zadanie nr 2.
Dany jest punkt \(A=(1,4)\). Znaleźć taki punkt \(B\), że \(|\overline{AB}|=1\) i który leży na prostej \(x=\frac{1}{2}\).
Zadanie nr 3.
Obliczyć pole i obwód trójkąta prostokątnego, wyznaczonego przez punkty \(A=(1,2), B=(1,3), C=(4,1)\).
Zadanie nr 4.
Dany jest odcinek o końcach \(A=(2+\sqrt{2}, 2), \ B=(-4+\sqrt{2}, -4)\). Znaleźć współrzędne środka odcinka \(\overline{AB}\).
Zadanie nr 5.
Znaleźć środek kwadratu wyznaczonego przez punkty \(A=(0,0), B=(1,2), C=(3,1), D=(2,-1)\).
Zadanie nr 6.
Znaleźć równanie symetralnej odcinka \(\overline{AB}\), gdzie \(A=(1,4), \ B=(-2, 1)\).

Zadanie nr 7 — maturalne.
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.

Zadanie nr 8 — maturalne.
Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(- 2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek).
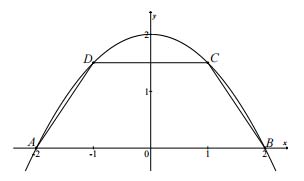
Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe.

Zadanie nr 9 — maturalne.
Odległość początku układu współrzędnych od prostej o równaniu \(y = 2x + 4\) jest równa
A. \(\frac{\sqrt{5}}{5}\)
B. \(\frac{4\sqrt{5}}{5}\)
C. \(\frac{4}{5}\)
D. \(4\)

Zadanie nr 10 — maturalne.
Punkt \(A=(7,−1)\) jest wierzchołkiem trójkąta równoramiennego \(ABC\), w którym \(|AC|=|BC|\). Obie współrzędne wierzchołka \(C\) są liczbami ujemnymi. Okrąg wpisany w trójkąt ABC ma równanie \(x^2+y^2=10\). Oblicz współrzędne wierzchołków \(B\) i \(C\) tego trójkąta.

Zadanie nr 11 — maturalne.
Dane są punkty o współrzędnych \(A=(−2, 5)\) oraz \(B=(4, −1)\). Średnica okręgu wpisanego
w kwadrat o boku \(AB\) jest równa
A. \(12\)
B. \(6\)
C. \(6\sqrt{2}\)
D. \(2\sqrt{6}\)

Zadanie nr 12 — maturalne.
Dany jest punkt \(A=(−18,10)\). Prosta o równaniu \(y=3x\) jest symetralną odcinka \(AB\). Wyznacz współrzędne punktu \(B\).

Zadanie nr 13 — maturalne.
Punkt B jest obrazem punktu \(A=(−3,5)\) w symetrii względem początku układu współrzędnych. Długość odcinka \(AB\) jest równa
A. \(2\sqrt{34}\)
B. \(8\)
C. \(\sqrt{34}\)
D. \(12\)

Zadanie nr 14 — maturalne.
Punkty \(K=(4,−10)\) i \(L=(b,2)\) są końcami odcinka \(KL\). Pierwsza współrzędna środka odcinka \(KL\) jest równa (−12). Wynika stąd, że
A. \(b=-28\)
B. \(b=-14\)
C. \(b=-24\)
D. \(b=-10\)

