Wartość bezwzględna
Definicja wartości bezwzględnej jest następująca:
Wartość bezwzględną liczby x oznaczamy symbolem \(|x|\) i określamy w następujący sposób:
Mówiąc inaczej, wartość bezwzględna liczby nieujemnej jest to ta sama liczba, natomiast wartość bezwzględna liczby ujemnej, to liczba do niej przeciwna.
Przykłady
Jak obliczyć wartość bezwzględną? Oto kilka przykładów:
- \(|3|=3\)
- \(|-3|=3\)
- \(|-\frac{5}{7}|=\frac{5}{7}\)
- \(|0|=0\)
Zauważmy, że wartość bezwzględna z 0 jest równa zeru.
Własności wartości bezwzględnej
Wartość bezwzględna ma następujące własności:
- \(|a|\geq0, |a| = 0 \Leftrightarrow a = 0\)
- \(|a| = |-a|\)
- \(|a\cdot b| = |a|\cdot |b|\)
- \(|\frac{a}{b}| = \frac{|a|}{|b|}, b\neq 0\)
- \(a\leq |a|\);
- \(|a+b| \leq |a| + |b|\)
- \(||a| - |b||\leq |a - b|\)
Interpretacja geometryczna wartości bezwzględnej
Zapis \(|a|\) można zinterpretować, jako odległość liczby a od początku układu współrzędnych.
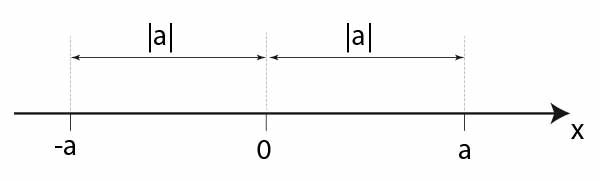
Z kolei zapis \(|a-b|\) interpretujemy jako odległość na osi liczbowej między punktami a i b.
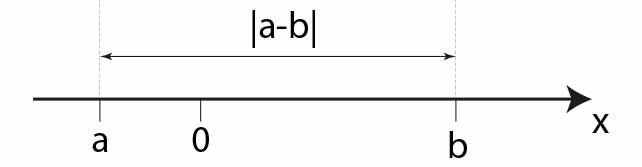
Obliczanie wartości bezwzględnej
Aby obliczyć wartość bezwzględną wyrażenia, należy ustalić, czy wyrażenie to jest dodatnie, czy ujemne. Jeżeli jest ujemne, to zmieniamy znak wyrażenia na przeciwny przy opuszczaniu symbolu wartości bezwzględnej.
Przykłady
1. Obliczmy \(|4-\sqrt{3}|\).
Szacujemy, że \(\sqrt{3}\approx 1,73\), więc gdy odejmiemy tę liczbę od 4, otrzymamy liczbę dodatnią. Możemy więc napisać, że:
\(|4-\sqrt{3}|=4-\sqrt{3}\)
2. Obliczmy \(|\sqrt{3}-4|\).
Szacujemy, że \(\sqrt{3}\approx 1,73\), więc gdy odejmiemy od tej liczby 4, otrzymamy liczbę ujemną, a zatem wyrażenie pod wartością bezwzględną jest mniejsze od zera — musimy zmienić znak podczas „opuszczania” wartości bezwzględnej. W tym przypadku musimy napisać, że: \(|\sqrt{3}-4|=-\sqrt{3}+4\)
Wartość bezwzględna a pierwiastek
Przyjrzyjmy się wyrażeniu: \(\sqrt{a^2}=a\). Jeżeli za a podstawimy na przykład liczbę 5, to otrzymamy zdanie prawdziwe. Kiedy natomiast do wyrażenia wstawimy za a liczbę -5, równości nie jest już prawdziwa. Obowiązuje zatem wyłącznie dla liczb nieujemnych. Z całą pewnością możemy zatem napisać, że:
Przykłady
Kiedy prawdziwa jest równość \(|a|=-a\)?
Na pierwszy rzut oka wydaje się, że nie ma takiej liczby, która spełniałaby powyższe równanie, gdyż wiemy, że wartość bezwzględna liczby jest zawsze dodatnia. Jednak w równaniu mamy do czynienia z wyrazem ogólnym a, który może przybierać różne wartości. Wyraz a nie zawsze oznacza liczbę dodatnią, natomiast -a nie musi oznaczać wartości ujemnej. Prawa strona równania jest dodatnia, kiedy za a podstawimy liczbę ujemną, np. -(-5) = 5. Zauważamy, że równanie jest w takim przypadku spełnione, bo np. |-5| = - (-5) = 5.
Zatem równanie jest spełnione dla liczb ujemnych.
Jak pozbyć się wartości bezwzględnej z równania?
Aby pozbyć się wartości bezwzględnej z dowolnego równania, korzystamy bezpośrednio z definicji wartości bezwzględnej. Mamy do rozpatrzenia dwa przypadki:
- przypadek pierwszy — gdy wyrażenie pod wartością bezwzględną jest nieujemne, wówczas możemy opuścić symbol wartości bezwzględnej podczas przepisywania równania;
- przypadek drugi — gdy wyrażenie pod wartością bezwzględną jest ujemne, wówczas zapisujemy wyrażenie przeciwne do tego, które znajduje się pod wartością bezwzględną.
Przykłady
\(|-x+1|=\begin{cases} -x+1 \text{ dla -x+1}\geq 0 \\x-1 \text{ dla -x+1<0}\end{cases}\)
Przykład, którym wartość bezwzględna jest tylko częścią wyrażenia:
\(|x^2-1|+x-1=\begin{cases} x^2-1+x-1 = x^2+x-2 \text{ dla }x^2-1\geq 0 \\-x^2+1+x-1 = -x^2+x \text{ dla } x^2-1<0\end{cases}\)
I jeszcze jeden ciekawy przykład:
\(|x^4+1|=x^4+1\)
Ponieważ \(x^4+1\) jest zawsze dodatnie, możemy pominąć w zapisie wartość bezwzględną.
Pytania
Czy wartość bezwzględna liczby i moduł to jest to samo?
Moduł liczby rzeczywistej i wartość bezwzględna liczby rzeczywistej ma tę samą wartość. Pojęcia „moduł” używa się w szerszym kontekście, bo także dla liczb zespolonych. Jednak i w tym przypadku można używać zamiennie tych terminów. Moduł odnosi się do miary długości odcinka. Staje się to jasne, gdy spojrzymy na interpretację geometryczną wartości bezwzględnej (patrz wyżej).
Jak obliczyć wartość bezwzględną w programie Excel?
Korzystamy z funkcji MODUŁ.LICZBY. Dla przykładu wpiszmy w dowolną komórkę formułę "=MODUŁ.LICZBY(-5)" i naciśnijmy ENTER. Otrzymamy wartość 5.
Jak obliczyć wartość bezwzględna do kwadratu?
\(|x|^2=x^2\)
Jak rozwiązywać równania z wartością bezwzględną?
Zagadnieniu temu poświęciliśmy osobne artykuły:
Zadania z rozwiązaniami

Zadanie nr 2 — maturalne.
Na osi liczbowej zaznaczono sumę przedziałów.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A. \(|x-3,5|\geq 1,5\)
B. \(|x-1,5|\geq 3,5\)
C. \(|x-3,5|\leq 1,5\)
D. \(|x-1,5|\leq 3,5\)

Zadanie nr 3 — maturalne.
Dla każdej liczby \(x\), spełniającej warunek \(-3<x<0\), wyrażenie \(\frac{|x+3|-x+3}{x}\) jest równe:
A. \(2\)
B. \(3\)
C. \(-\frac{6}{x}\)
D. \(\frac{6}{x}\)

Zadanie nr 10 — maturalne.
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność \(|2x-8|\leq 10\)

Stąd wynika, że
A. \(k=2\)
B. \(k=4\)
C. \(k=5\)
D. \(k=9\)
Powiązane materiały
 Wartość bezwzględna
Wartość bezwzględna© medianauka.pl, 2009-03-13, A-165
Data aktualizacji artykułu: 2023-03-27

 Wartość bezwzględna
Wartość bezwzględna Równania z wartością bezwzględną
Równania z wartością bezwzględną Nierówności z wartością bezwzględną
Nierówności z wartością bezwzględną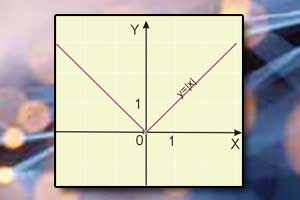 Wykres funkcji z wartością bezwzględną
Wykres funkcji z wartością bezwzględną Wartość bezwzględna — quiz
Wartość bezwzględna — quiz