Wykres funkcji logarytmicznej

Wykres funkcji logarytmicznej nosi nazwę krzywej logarytmicznej. Wykresy funkcji logarytmicznej różnią się znacznie w przypadku, gdy podstawa logarytmu jest większa lub mniejsza od jedności.

Przykład

Sporządzimy wykres funkcji
$y=\log_{2}{x},\quad{}y=\log_{\frac{1}{2}}{x}$ .

Sporządzamy najpierw tabelkę zmienności tych funkcji:

x	1/4	1/2	1	2	4
$y=\log_{2}{x}$	-2	-1	0	1	2
$y=\log_{\frac{1}{2}}{x}$	2	1	0	-1	-2

i szkicujemy wykresy obu funkcji

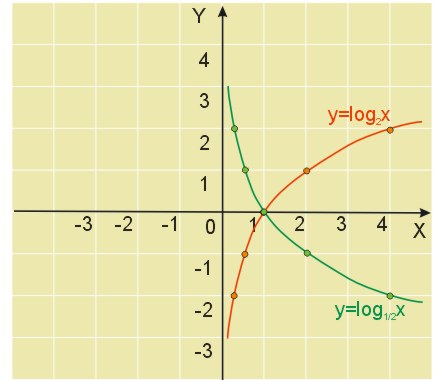
Warto dodać, że wykres funkcji logarytmicznej o podstawie a jest symetryczny względem prostej y=x do wykresu funkcji wykładniczej o podstawie a.

Zauważ, że funkcja ta ma jedno miejsce zerowe x₀=1.

Wykres Wykres funkcji logarytmicznej - symulacja

Poniższa symulacja pozwala zaobserwować zachowanie się wykresu funkcji logarytmicznej w zależności od wartości współczynnika a - podstawy logarytmu

Funkcja w postaci y = log_ax, czyli y =

a 1

Zadania z rozwiązaniami

Zadania związane z tematem:
Wykres funkcji logarytmicznej

Zadanie - wykres funkcji logarytmicznej
Naszkicować wykres funkcji $y=\log_{\frac{1}{3}}{(x-3)}+1$

Pokaż rozwiązanie zadania

Zadanie - sporządzanie wykresu funkcji logarytmicznej
Naszkicować wykres funkcji $y=\log_{2}{4x}$

Pokaż rozwiązanie zadania

Zadanie - szkicowanie wykresu funkcji logarytmicznej
Naszkicować wykres funkcji $y=\log_{\frac{1}{2}}{(\sqrt{2}x+2\sqrt{2})}+1$

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Funkcja logarytmiczna
Funkcja logarytmiczna jest to funkcja w postaci y=log_ax

Test wiedzy
Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.

Wykres funkcji logarytmicznej

Funkcja w postaci y = logax, czyli y =

Zadania z rozwiązaniami

Inne zagadnienia z tej lekcji

Funkcja w postaci y = log_ax, czyli y =