Równanie kwadratowe z parametrem
Czasem w równaniach stosuje się oznaczenia literowe, nazywane parametrami, a równanie zawierające takie oznaczenia literowe nazywamy równaniem z parametrem. Zawsze w takim równaniu musimy wskazać niewiadomą lub ze względu na jaką zmienną należy rozwiązać dane równanie. Parametryzujemy równania w celu ich uogólnienia. Rozwiązując równanie z parametrem, rozwiązujemy całą grupę (klasę) równań.
Poniżej przykład zadania, w którym używa się parametru.
Zadanie 1
Rozwiązać równanie ze względu na zmienną x.
\((m-1)x^2+x+3=0\)
Aby powyższe równanie mogło być równaniem kwadratowym, wartość współczynnika przy drugiej potędze x musi być różna od zera:
\(m-1\neq{0}\)
\(m\neq{1}\)
Dla \(m=1\) mamy równanie liniowe \(x+3=0\), którego rozwiązaniem jest liczba (-3).
Zajmijmy się jednak przypadkiem równania kwadratowego. Mamy tutaj:
\(a=m-1, b=1, c=3\)
Obliczamy wyróżnik \(\Delta=b^2-4ac=1-12(m-1)=1-12m+12=-12m+13\).
Możliwe są trzy przypadki. Musimy je wszystkie rozpatrzyć.
- Jeżeli \(\Delta>0\Leftrightarrow{-12m+13>0} \Leftrightarrow {12m<13}\Leftrightarrow{m<1\frac{1}{12}}\), równanie ma dwa pierwiastki rzeczywiste:
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-1-\sqrt{13-12m}}{2(m-1)}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-1+\sqrt{13-12m}}{2(m-1)}\) - Jeżeli \(\Delta=0\Leftrightarrow{-12m+13=0} \Leftrightarrow {m=1\frac{1}{12}}\) równanie ma jeden podwójny pierwiastek rzeczywisty:
\(x_0=\frac{-b}{2a}=-\frac{1}{2(m-1)}\) - Jeżeli \(\Delta<0\Leftrightarrow{m>1\frac{1}{12}}\) równanie nie ma rozwiązania w zbiorze liczb rzeczywistych.
Rozwiązanie takiego równania jest dość skomplikowane, jednak opłaca się to. Zauważ, że tak naprawdę rozwiązaliśmy nieskończenie wiele różnych równań kwadratowych i jedno liniowe, gdyż za parametr \(m\) możemy podstawić dowolną liczbę rzeczywistą!
Oto inny, bardziej złożony przykład.
Zadanie 2
Rozwiązać równanie ze względu na zmienną \(x\) przy założeniu, że parametr \(k\) jest różny od zera \(kx^2+x+k=0\).
Powyższe równanie jest równaniem kwadratowym, ponieważ \(k\) jest różne od zera. Mamy tutaj:
\(a=k, b=1, c=k\)
Obliczamy wyróżnik \(\Delta=b^2-4ac=1-4k^2=-4(k^2-\frac{1}{4})=-4(k-\frac{1}{2})(k+\frac{1}{2})\).
Rozłożyliśmy wyróżnik na czynniki liniowe, aby łatwiej można było badać jego znak.
Możliwe są trzy przypadki. Musimy je wszystkie rozpatrzyć. Wcześniej warto sporządzić szkic wykresu, na podstawie którego można odczytać rozwiązanie. Mamy już miejsca zerowe: \(\frac{1}{2}\) i \(-\frac{1}{2}\), ponieważ \(a=-4<0\), więc ramiona paraboli skierowane są w dół.
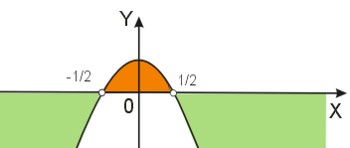
- Jeżeli \(\Delta>0\Leftrightarrow{-4(k-\frac{1}{2})(k+\frac{1}{2})>0}\), czyli dla \(k\in(-\frac{1}{2};\frac{1}{2})\) równanie ma dwa pierwiastki rzeczywiste:
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-1-\sqrt{1-4k^2}}{2k}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-1+\sqrt{1-4k^2}}{2k}\) - Jeżeli \(\Delta=0\Leftrightarrow{k=-\frac{1}{2}}\quad{lub}\quad{m}=\frac{1}{2}\), równanie ma jeden podwójny pierwiastek rzeczywisty:
\(x_0=\frac{-b}{2a}=-\frac{1}{2k}\) - Jeżeli \(\Delta<0\Leftrightarrow{-4(k-\frac{1}{2})(k+\frac{1}{2})<0}\), czyli dla \(k\in(-\infty;-\frac{1}{2})\cup(\frac{1}{2};+\infty)\) równanie nie ma rozwiązania w zbiorze liczb rzeczywistych.
Zadania z rozwiązaniami

Zadanie nr 1.
Dla jakiej wartości parametru \(m\) równanie \(mx^2+4mx-m+1=0\) ma jedno rozwiązanie? Znajdź to rozwiązanie?

Zadanie nr 2.
Dla jakich wartości parametru \(m\) suma odwrotności pierwiastków równania \(x^2-2(m+1)x+(m^2+3m-18)=0\) ma wartość ujemną?

Zadanie nr 3.
Rozwiązać równanie \(\frac{3}{x-a}=\frac{x+a}{1-x}\) w zależności od parametru \(a\).

Zadanie nr 4.
Rozwiązać równanie \(\frac{2}{x-a}=\frac{x-a}{x}\) w zależności od parametru \(a\).

Zadanie nr 5.
Określić liczbę rozwiązań równania \((a+3)x^2-(a+1)x+1=0\) w zależności od parametru \(a\).

Zadanie nr 6.
Dla jakiej wartości parametru \(m\) równanie \(m^2x^2-6x+9=0\) ma jedno rozwiązanie?

Zadanie nr 7.
Znaleźć taką wartość parametru m, dla której suma kwadratów pierwiastków równania \(x^2-mx-m-1=0\) jest najmniejsza.

Zadanie nr 8 — maturalne.
Dany jest trójmian kwadratowy \(f(x)=x^2+2(m+1)x+6m+1\). Wyznacz wszystkie rzeczywiste wartości parametru m, dla których ten trójmian ma dwa różne pierwiastki \(x_1\), \(x_2\) tego samego znaku, spełniające warunek \(|x_1-x_2|<3\).

Zadanie nr 9 — maturalne.
Dany jest trójmian kwadratowy \(f(x)=(m+1)x^2+2(m-2)x-m+4\). Wyznacz wszystkie wartości parametru \(m\), dla których trójmian \(f\) ma dwa różne pierwiastki rzeczywiste \(x_1, x_2\), spełniające warunek \(x_1^2-x_2^2=x_1^4-x_2^4\).

Zadanie nr 10 — maturalne.
Wyznacz wszystkie wartości parametru \(m\), dla których trójmian kwadratowy \(4x^2-2(m+1)x+m\) ma dwa różne pierwiastki rzeczywiste \(x_1\) oraz \(x_2\), spełniające warunki: \(x_1 \neq 0, x_2\neq 0\) oraz \(x_1+x_2\leq \frac{1}{x_1}+\frac{1}{x_2}\).
Inne zagadnienia z tej lekcji
© medianauka.pl, 2009-08-15, A-274
Data aktualizacji artykułu: 2023-05-07

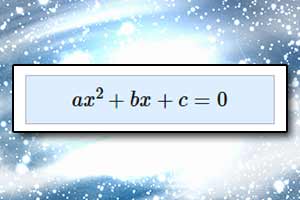 Równanie kwadratowe
Równanie kwadratowe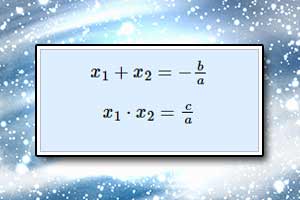 Wzory Viete'a
Wzory Viete'a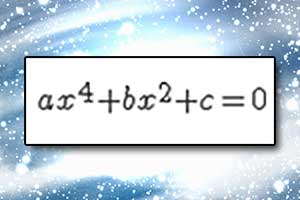 Równanie dwukwadratowe
Równanie dwukwadratowe