Logika i zbiory

Ten dział niniejszego kursu zawiera podstawowe informacje z dziedziny logiki matematycznej, zajmujemy się tu także zbiorami i działaniami na zbiorach. Mimo, że teoria mnogości i logika matematyczna to dwie odrębne dyscypliny, to z uwagi na ich bliskość, a także z uwagi na stanowienie podwalin i dostarczanie narzędzi dla pozostałych dyscyplin matematyki, prezentujemy je w niniejszym kursie łącznie.

Spis treści

Logika matematyczna

Logika matematyczna to dział matematyki,który zajmuje się badaniem struktur, metod i innych własności teorii matematycznych. Omawiamy tutaj rachunek zdań, kwantyfikatory, indukcję matematyczną i inne zagadnienia, stanowiące podstawę matematyki. Niegdyś logika matematyczna stanowiła dział pomocniczy matematyki. Na początku XX wieku uzyskała status samodzielnej dyscypliny matematyki. Najbardziej znani naukowcy tej dziedziny nauki to Gottlob Frege, Giuseppe Peano, Bertrand Russell, a także polscy naukowcy Jan Łukasiewicz oraz Alfred Tarski.

Zdanie logiczne
Zdanie w logice jest to zdanie oznajmujące, któremu można przypisać prawdę lub fałsz.

Negacja
Negacja (~p), nazywana też zaprzeczeniem logicznym to zdanie: "nieprawda, że p".

Koniunkcja, iloczyn logiczny
Koniunkcją nazywamy zdanie "p i q" i oznaczamy p ∧ q

Alternatywa, suma logiczna
Alternatywą lub sumą logiczną nazywamy zdanie "p lub q" i oznaczamy p ∨ q

Równoważność zdań
Równoważność zdań p i q jest to zdanie orzekające, że zdania p i q mają tę samą wartość logiczną.

I prawo de Morgana
Zaprzeczenie koniunkcji dwóch zdań logicznych jest równoważne alternatywie zaprzeczeń tych zdań.

II prawo de Morgana
Zaprzeczenie alternatywy dwóch zdań logicznych jest równoważne koniunkcji zaprzeczeń tych zdań.

Implikacja
Implikacją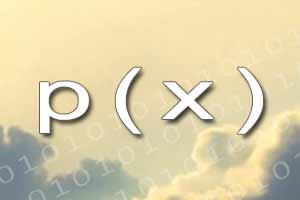 (wynikaniem) nazywamy zdanie "jeżeli p, to q" i zapisujemy: p ⇒ q.

Warunek konieczny i wystarczający
Co to jest warunek konieczny i wystarczający w logice matematycznej?

Forma zdaniowa
co to jest forma zdaniowa zmiennej x?

Kwantyfikatory
Kwantyfikatory są to zwroty rodzaju: dla każdego x ... istnieje takie x, że ...

Definicja
Co to jest pojęcie pierwotne i definicja?

Aksjomaty i twierdzenia
Co to jest aksjomat i twierdzenie, teza i założenie?

Indukcja matematyczna
Indukcja matematyczna (zupełna) jest to metoda dowodzenia twierdzeń o liczbach naturalnych.

Elementy logiki - część 1

Elementy logiki - część 2

Dowody i twierdzenia

SPIS TREŚCI

Zbiory

Zbiór to podstawowe pojęcie w matematyce. To pojęcie pierwotne, nie podlegające definicji. Stanowi podstawę teorii mnogości (teorii zbiorów). Omawiamy tu podstawowe pojęcia związane ze zbiorami i ilustrujemy podstawowe działania na zbiorach. Za twórcę teorii zbiorów (mnogości) uważa się Georga Cantora (1845-1918). To dziś podstawowa dyscyplina matematyki, która stanowi niezbędne narzędzie dla pozostałych dziedzin matematycznych.

Zbiór
Zbiór, inaczej mnogość jest pojęciem pierwotnym w matematyce. Rodzaje i oznaczanie zbiorów. Moc zbioru.

Podzbiory
Zawieranie się zbiorów oraz pojęcie podzbioru i równości zbiorów.

Suma zbiorów
Jak tworzyć sumę zbiorów? Własności oraz przykłady sumy zbiorów.

Różnica zbiorów
Jak tworzyć różnicę zbiorów? Własności oraz przykłady różnicy zbiorów.

Iloczyn zbiorów
Jak tworzyć część wspólną zbiorów? Własności oraz przykłady iloczynu zbiorów.

Iloczyn kartezjański
Co to jest i jak stworzyć iloczyn kartezjański zbiorów?

Zbiory i działania na zbiorach

SPIS TREŚCI