Zadania — matura 2015, matematyka, poziom rozszerzony

Zadanie nr 1 - maturalne.

<p>Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność \(|2x-8|\leq 10\)</p> <p><img src="matematyka/grafika/zmr1-2015.jpg" class="skaluj m10" alt="rysunek , zadanie maturalne 1/2015"></p> <p>Stąd wynika, że</p> <p>A. \(k=2\)</p> <p>B. \(k=4\)</p> <p>C. \(k=5\)</p> <p>D. \(k=9\)</p>

Pokaż rozwiązanie zadania.

Zadanie nr 2 - maturalne.

<p>Dana jest funkcja \(f\) określona wzorem</p> <p>\(f(x)=\begin{cases}x-2 \quad dla \quad x\leq0\\||x+3|-4| \quad dla \quad x&gt;0 \end{cases}\).</p> <p>Równanie \(f(x)=1\) ma dokładnie</p> <p>A. jedno rozwiązanie.</p> <p>B. dwa rozwiązania.</p> <p>C. cztery rozwiązania.</p> <p>D. pięć rozwiązań.</p>

Pokaż rozwiązanie zadania.

Zadanie nr 3 - maturalne.

<p>Liczba \((3-2\sqrt{3})^3\) jest równa:</p> <p>A. \(27-24\sqrt{3}\)</p> <p>B. \(27-30\sqrt{3}\)</p> <p>C. \(135-78\sqrt{3}\)</p> <p>D. \(135-30\sqrt{3}\)</p>

Pokaż rozwiązanie zadania.

Zadanie nr 4 - maturalne.

<p>Równanie \(2sinx+3cosx=6\) w przedziale \((0,2\pi)\) </p> <p>A. nie ma rozwiązań rzeczywistych.</p> <p>B. ma dokładnie jedno rozwiązanie rzeczywiste.</p> <p>C. ma dokładnie dwa rozwiązania rzeczywiste.</p> <p>D. ma więcej niż dwa rozwiązania rzeczywiste.</p>

Pokaż rozwiązanie zadania.

Zadanie nr 5 - maturalne.

<p>Odległość początku układu współrzędnych od prostej o równaniu \(y = 2x + 4\) jest równa</p> <p>A. \(\frac{\sqrt{5}}{5}\)</p> <p>B. \(\frac{4\sqrt{5}}{5}\)</p> <p>C. \(\frac{4}{5}\)</p> <p>D. \(4\)</p>

Pokaż rozwiązanie zadania.

Zadanie nr 6 - maturalne.

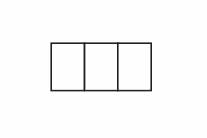
<p>Oblicz granicę \(\displaystyle\lim_{n\to \infty}(\frac{11n^3+6n+5}{6n^3+1}-\frac{2n^2+2n+1}{5n^2-4})\). W poniższe kratki wpisz kolejno cyfrę jedności i pierwsze dwie cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.</p> <p><img src="matematyka/grafika/zadania/0075.jpg" width="207" height="138" alt="kratki"></p>

Pokaż rozwiązanie zadania.

Zadanie nr 7 - maturalne.

<p>Liczby \((-1)\) i \(3\) są miejscami zerowymi funkcji kwadratowej \(f\). Oblicz \(\frac{f(6)}{f(12)}\).</p>

Pokaż rozwiązanie zadania.

Zadanie nr 8 - maturalne.

<p>Udowodnij, że dla każdej liczby rzeczywistej \(x\) prawdziwa jest nierówność \(x^4-x^2-2x+3&gt;0\).</p>

Pokaż rozwiązanie zadania.

Zadanie nr 9 - maturalne.

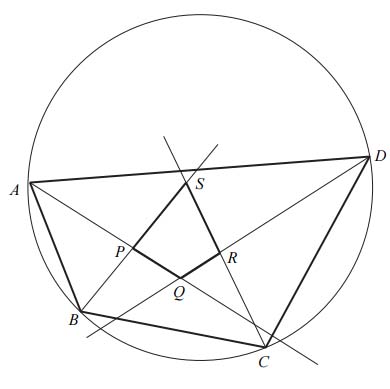
<p>Dwusieczne czworokąta \(ABCD\) wpisanego w okrąg przecinają się w czterech różnych punktach: \(P, Q, R, S\) (zobacz rysunek).</p> <p><img src="matematyka/grafika/zmr9-2015.jpg" width="390" height="389" alt="rysunek do zanaia 9, matura 2015"></p> <p>Wykaż, że na czworokącie \(PQRS\) można opisać okrąg.</p>

Pokaż rozwiązanie zadania.

Zadanie nr 10 - maturalne.

<p>Długości boków czworokąta \(ABCD\) są równe: \(|AB|=2, |BC|=3, |CD|=4, |DA|=5\). Na czworokącie \(ABCD\) opisano okrąg. Oblicz długość przekątnej \(AC\) tego czworokąta.</p>

Pokaż rozwiązanie zadania.

Zadanie nr 11 - maturalne.

<p>W pierwszej urnie umieszczono 3 kule białe i 5 kul czarnych, a w drugiej urnie 7 kul białych i 2 kule czarne. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo dokładamy do urny drugiej jeszcze dwie kule tego samego koloru, co wylosowana kula. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą białe.</p>

Pokaż rozwiązanie zadania.

Zadanie nr 12 - maturalne.

<p>Funkcja \(f\) określona jest wzorem \(f(x)=x^3-2x^2+1\) dla każdej liczby rzeczywistej \(x\). Wyznacz równania tych stycznych do wykresu funkcji \(f\), które są równoległe do prostej o równaniu \(y=4x\).</p>

Pokaż rozwiązanie zadania.

Zadanie nr 13 - maturalne.

<p>Dany jest trójmian kwadratowy \(f(x)=(m+1)x^2+2(m-2)x-m+4\). Wyznacz wszystkie wartości parametru \(m\), dla których trójmian \(f\) ma dwa różne pierwiastki rzeczywiste \(x_1, x_2\), spełniające warunek \(x_1^2-x_2^2=x_1^4-x_2^4\).</p>

Pokaż rozwiązanie zadania.

Zadanie nr 14 - maturalne.

<p>Podstawą ostrosłupa \(ABCDS\) jest kwadrat \(ABCD\). Krawędź boczna \(SD\) jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi \(ABS\) i \(CBS\) tego ostrosłupa.

Pokaż rozwiązanie zadania.

Zadanie nr 15 - maturalne.

<p>Suma wszystkich czterech współczynników wielomianu \(W(x)=x^3+ax^2+bx+c\) jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej \(3\). Oblicz współczynniki \(a\), \(b\) i \(c\). Rozważ wszystkie możliwe przypadki.</p>

Pokaż rozwiązanie zadania.

Zadanie nr 16 - maturalne.

<p>Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.</p>

Pokaż rozwiązanie zadania.