Równanie kwadratowe
Co to jest równanie kwadratowe? Jest to równanie w postaci
gdzie \(a\neq{0}\), \(b, c\) — są dowolnymi liczbami rzeczywistymi, nazywamy równaniem kwadratowym lub równaniem drugiego stopnia.
Jest to postać ogólna równania kwadratowego.
Przykłady
Przykładów równań kwadratowych:
- \(2x^2-3x+6=0\)
- \(-x^2-x+5=0\)
- \(5x^2+5=0\)
- \(-4x^2-5x=0\)
- \(x^2=0\)
Niżej wymienione równania również są równaniami kwadratowymi. Dopiero po ich przekształceniu otrzymamy postać \(ax^2+b+c=0\).
- \(x(x-1)=0\)
- \((x-1)(x+1)=0\)
- \(-5(1+x)(\sqrt{7}-x)=1\)
Rozwiązywanie równań kwadratowych
Ponieważ równanie kwadratowe to nic innego jak trójmian kwadratowy przyrównany do zera, dyskusja liczby rozwiązań (pierwiastków) równania sprowadza się do dyskusji liczby punktów zerowych funkcji kwadratowej.
Równanie kwadratowe — wzory
Zatem w zależności od wyróżnika:
Mamy trzy możliwości:
- Jeżeli \(\Delta>0\), to równanie kwadratowe ma dwa rozwiązania (pierwiastki równania kwadratowego):\(x_1=\frac{-b-\sqrt{\Delta}}{2a},\quad{x_2}=\frac{-b+\sqrt{\Delta}}{2a}\)
- Jeżeli \(\Delta=0\), to równanie kwadratowe ma jeden pierwiastek (zwany podwójnym):
\(x_0=-\frac{b}{2a}\) - Jeżeli \(\Delta<0\), to równanie kwadratowe nie ma pierwiastków rzeczywistych.
Powyższe wzory będą wykorzystywane przy rozwiązywaniu większości równań kwadratowych. Jak rozwiązać równanie kwadratowe? Wystarczy wyznaczyć pierwiastek równania kwadratowego lub oba pierwiastki z wykorzystaniem wyżej podanych wzorów.
Kalkulator równań kwadratowych
Rozwiązywanie równań kwadratowych online
Nasz kalkulator spróbuje rozwiązać dowolne równanie kwadratowe w postaci \(ax^2+bx+c=0\). Aby rozwiązać równanie swoje równanie kwadratowe, podaj współczynniki \(a\),\(b\) i \(c\):
Wpisz dane:\(x^2+\) \(x\) \(=0\)
Inne kalkulatory: wykaz wszystkich kalkulatorów
Przykładowe zadania
Oto kilka przykładów rozwiązań równań kwadratowych.
Zadanie 1
Rozwiązać równanie kwadratowe \(x^2+3x-4=0\).
\(a=1, b=3, c=-4\)
Obliczamy wyróżnik
\(\Delta=b^2-4ac=3^2-4\cdot{1}\cdot{(-4)}=9+16=25\)
Wyróżnik jest większy od zera, więc równanie ma dwa pierwiastki.
\(\sqrt{\Delta}=5\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-3-5}{2}=-4\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-3+5}{2}=1\)
Odpowiedź: \(x_1=-4,\quad{x_2=1}\)
Zadanie 2
Rozwiązać równanie \(-x^2+6x-9=0\).
Mamy:
\(a=-1, b=6, c=-9\)
Obliczamy wyróżnik
\(\Delta=b^2-4ac=6^2-4\cdot{(-1)}\cdot{(-9)}=36-36=0\)
Wyróżnik jest równy zero, więc równanie ma jeden podwójny pierwiastek.
\(x_0=\frac{-b}{2a}=\frac{-6}{-2}=3\)
Odpowiedź: \(x_0=3\)
Zadanie 3
Rozwiązać równanie kwadratowe \(x^2+3=0\).
Mamy
\(a=1, b=0, c=3\)
Obliczamy wyróżnik
\(\Delta=b^2-4ac=0-4\cdot{1}\cdot{3}=-12\)
Wyróżnik jest ujemny, więc równanie nie ma pierwiastków rzeczywistych.
Odpowiedź: Równanie nie ma rozwiązania.
Równania kwadratowe w postaci iloczynowej
Jeżeli mamy do czynienia z równaniem w postaci \(a(x-x_1)(x-x_2)=0\), gdzie a jest różną od zera liczbą rzeczywistą, to liczby \(x_1, x_2\) są pierwiastkami (rozwiązaniami) tego równania.
W ten sposób możemy bardzo szybko rozwiązać równanie kwadratowe. Jeżeli tylko potrafimy dany trójmian kwadratowy za pomocą wzorów skróconego mnożenia albo poprzez wyłączenie przed nawias wyrażenia sprowadzić dane równanie do postaci iloczynowej.
Przykład 1
Rozwiązać równanie \(2x^2-16x=0\).
Wyłączamy przed nawias wyrażenie \(2x\).
\(2x(x-8)=0\)
\(2(x-0)(x-8)=0\)
Odpowiedź:\(x_1=0, x_2=8\).
Przykład 2
Rozwiązać równanie \(3x^2-6x+3=0\).
Wyłączamy przed nawias liczbę \(2\).
\(3(x^2-2x+1)=0\)
W nawiasie mamy wyrażenie, dla którego wprost możemy zastosować wzór skróconego mnożenia.
\(3(x-1)^2=0\)
Odpowiedź:\(x_0=1\).
dlaczego mamy jeden pierwiastek? Można zapisać nasze równanie w postaci \(3(x-1)(x-1)=0\). Mamy więc dwa pierwiastki, które są sobie równe. Mówimy czasem, że równanie ma jeden podwójny pierwiastek.
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami
Zadanie nr 2.
Rozwiązać równanie kwadratowe:
a) \(x^2+4x-5=0\)
b) \(x^2-22x+121=0\)
c) \(x^2+2x+7=0\)
Zadanie nr 3.
Rozwiązać równanie:
a) \(x^2-\frac{1}{4}x-\frac{1}{8}=0\)
b) \(x^2-10x-119=0\)
Zadanie nr 4.
Znaleźć wszystkie równania kwadratowe, których rozwiązaniem są liczby \(\sqrt{2}, \ \frac{1}{2}\).
Zadanie nr 8 — maturalne.
Turysta zwiedzał zamek stojący na wzgórzu. Droga łącząca parking z zamkiem ma długość 2,1 km. Łączny czas wędrówki turysty z parkingu do zamku i z powrotem, nie licząc czasu poświęconego na zwiedzanie, był równy 1 godzinę i 4 minuty. Oblicz, z jaką średnią prędkością turysta wchodził na wzgórze, jeżeli prędkość ta była o 1 km/h mniejsza od średniej prędkości, z jaką schodził ze wzgórza.
Zadanie nr 9 — maturalne.
Równość \((x\sqrt{2} - 2)^2 = (\sqrt{2} + 2)^2\) jest
A. prawdziwa dla \(x=\sqrt{2}\)
B. prawdziwa dla \(x=-\sqrt{2}\)
C. prawdziwa dla \(x=-1\)
D. fałszywa dla każdej liczby \(x\)
Zadanie nr 10 — maturalne.
W każdym n-kącie wypukłym (n≥ 3) liczba przekątnych jest równa n(n-3)/2. Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
A. siedmiokąt.
B. dziesięciokąt.
C. dwunastokąt.
D. piętnastokąt.
Inne zagadnienia z tej lekcji
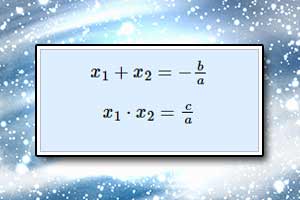Wzory Viete'a
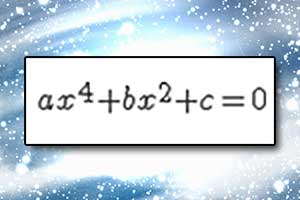Równanie dwukwadratowe
Równanie kwadratowe z parametrem
Równanie kwadratowe — podstawy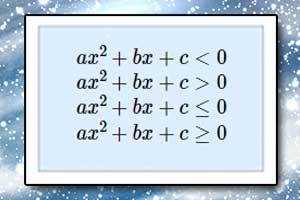
Nierówność kwadratowa© medianauka.pl, 2009-07-20, A-271
Data aktualizacji artykułu: 2023-05-06