Ostrosłup
Co to jest ostrosłup? Oto definicja ostrosłupa.
Jeżeli punkty \(A_1, A_2,...,A_n\), leżące w jednej płaszczyźnie \(\delta\), które wraz z punktem \(W\) leżącym poza nią określają kąt wielościenny, to iloczyn obszaru kąta wielościennego i półprzestrzeni domkniętej, mającej płaszczyznę brzegową \(\delta\) i zawierającej punkt \(W\), nazywamy ostrosłupem o podstawie \(A_1, A_2,...,A_n\) i wierzchołku \(W\).
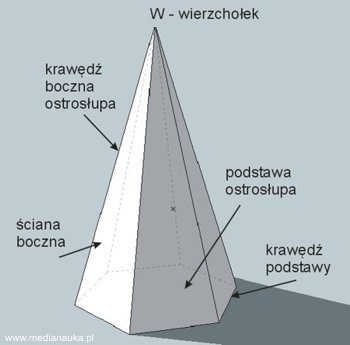
Rysunek ilustruje ostrosłup i nazwy poszczególnych jego elementów.
Własności ostrosłupa
- Wszystkie ściany boczne ostrosłupa są trójkątami.
- Ostrosłup jest wielościanem.
Objętość ostrosłupa
Jak obliczyć objętość ostrosłupa?
Objętość ostrosłupa (prostego lub pochyłego) jest równa trzeciej części iloczynu pola podstawy \(_+p\) i wysokości \(h\).
Wzór na objętość ostrosłupa:
Pole powierzchni ostrosłupa
Pole powierzchni ostrosłupa \(P\) jest równe sumie pola powierzchni podstawy \(P\) oraz pola powierzchni ścian bocznych \(P_b\).
Wzór na pole powierzchni ostrosłupa:
Wysokość ostrosłupa
Wysokość ostrosłupa \(h\) jest to odcinek poprowadzony z wierzchołka ostrosłupa prostopadle do płaszczyzny podstawy.
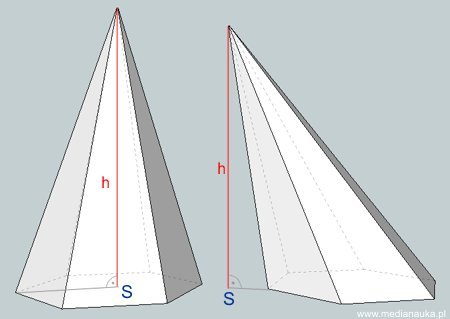
Spodek wysokości
Spodek wysokości \(S\) ostrosłupa to rzut prostokątny wierzchołka na płaszczyznę podstawy. Jak pokazuje poniższy rysunek, spodek nie musi leżeć w obrębie podstawy ostrosłupa.
Rodzaje ostrosłupów
Ostrosłup trójkątny, czworokątny, pięciokątny itd. to taki ostrosłup, którego liczba boków podstawy wynosi odpowiednio trzy, cztery, pięć itd.
Ostrosłup prawidłowy
Ostrosłup prawidłowy jest to ostrosłup, którego podstawą jest wielokąt foremny, a spodek wysokości leży w środku okręgu opisanego na podstawie tego ostrosłupa.
W ostrosłupie prawidłowym ściany boczne są trójkątami równobocznymi przystającymi do siebie.
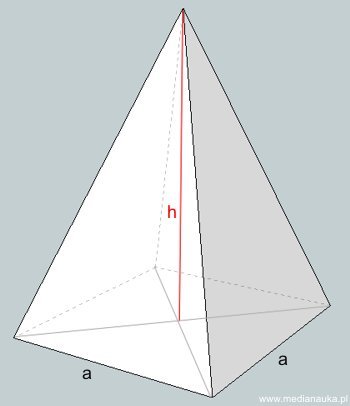
Poniższy rysunek przedstawia ostrosłup prawidłowy czworokątny — jest to piramida.
Czworościan
Czworościan jest to ostrosłup, którego podstawą jest trójkąt.
Każda ściana w czworościanie może być uważana za podstawę.
Czworościan foremny
Czworościan foremny to czworościan, którego wszystkie cztery ściany są trójkątami równobocznymi przystającymi do siebie wzajemnie.
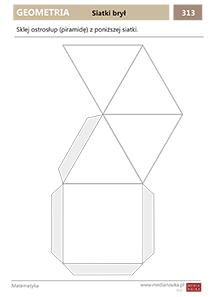
Na końcu artykułu znajduje się plik PDF — siatka czworościanu foremnego do sklejenia.
Ostrosłup ścięty
Ostrosłup ścięty jest to część ostrosłupa zawarta pomiędzy podstawą tego ostrosłupa i jego przekrojem poprzecznym.
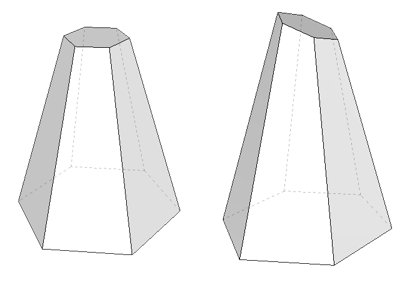
Ostrosłup może być ścięty równolegle i nierównolegle. Podstawy ostrosłupa ściętego są figurami podobnymi. Boczne ściany ostrosłupa ściętego są trapezami.
Ostrosłup ścięty jest prawidłowy (podstawą jest wielokąt foremny), jeśli powstał z ostrosłupa prawidłowego. W takim ostrosłupie ściętym ściany boczne są trapezami równoramiennymi, a wszystkie krawędzie boczne są równe.
Pole powierzchni ostrosłupa ściętego
Pole powierzchni ostrosłupa ściętego jest równe polu powierzchni podstaw tego ostrosłupa i ścian bocznych.
Objętość ostrosłupa ściętego
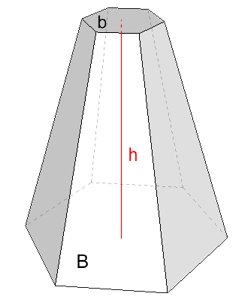
Jeżeli przez \(h\) oznaczymy wysokość ostrosłupa ściętego, przez \(B\) pole podstawy dolnej, \(b\) — pole podstawy górnej, to objętość ostrosłupa ściętego (równolegle) wyraża się wzorem:
Siatka ostrosłupa
Jak zrobić ostrosłup z papieru? Gotowe szablony siatki ostrosłupów do druku i sklejenia znajdziesz na końcu artykułu w formacie PDF w formie kart pracy.
Pytania
Ile ścian ma ostrosłup?
Ostrosłup o podstawie, która jest N-kątem ma N+1 ścian.
Co to jest ostrosłup prawidłowy czworokątny?
Jest to ostrosłup, którego podstawą jest kwadrat, a spodek wysokości leży na przecięciu przekątnych podstawy. Inn nazwa tej bryły to piramida.
Jaki ostrosłup ma 101 ścian?
To ostrosłup, który ma 100-kąt w podstawie.
Ile krawędzi ma ostrosłup?
Ostrosłup o podstawie, która jest N-kątem ma 2N krawędzi. Na przykład ostrosłup, który ma pięciokąt w podstawie ma 10 krawędzi.
Ile wierzchołków ma ostrosłup?
Ostrosłup o podstawie, która jest N-kątem ma N+1 wierzchołków. Na przykład ostrosłup, który ma pięciokąt w podstawie ma 6 wierzchołków.
Ćwiczenia
Ćwiczenia interakcyjne pomogą przygotować się na sprawdzian, test, egzamin, a ponadto usystematyzują wiedzę z danej dziedziny. To także świetny trening do matury. Wiele ćwiczeń to dobre zadania maturalne.
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
Podstawą ostrosłupa prawidłowego trójkątnego \(ABCS\) jest trójkąt równoboczny \(ABC\). Wysokość \(SO\) tego ostrosłupa jest równa wysokości jego podstawy. Objętość tego ostrosłupa jest równa 27. Oblicz pole powierzchni bocznej ostrosłupa \(ABCS\) oraz cosinus kąta, jaki tworzą wysokość ściany bocznej i płaszczyzna podstawy ostrosłupa.

Zadanie nr 2 — maturalne.
W ostrosłupie prawidłowym czworokątnym \(ABCDS\) o podstawie \(ABCD\) wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 120°. Oblicz objętość tego ostrosłupa.

Zadanie nr 3 — maturalne.
Podstawą ostrosłupa \(ABCDS\) jest kwadrat \(ABCD\). Krawędź boczna \(SD\) jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi \(ABS\) i \(CBS\) tego ostrosłupa.

Zadanie nr 4 — maturalne.
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa:
A. 5
B. 7
C. 8
D. 10

Zadanie nr 5 — maturalne.
Stożek i walec mają takie same podstawy i równe pola powierzchni bocznych. Wtedy tworząca stożka jest:
A. sześć razy dłuższa od wysokości walca.
B. trzy razy dłuższa od wysokości walca.
C. dwa razy dłuższa od wysokości walca.
D. równa wysokości walca.

Zadanie nr 6 — maturalne.
Podstawą ostrosłupa jest kwadrat \(KLMN\) o boku długości \(4\). Wysokością tego ostrosłupa jest krawędź \(NS\), a jej długość też jest równa \(4\) (zobacz rysunek).
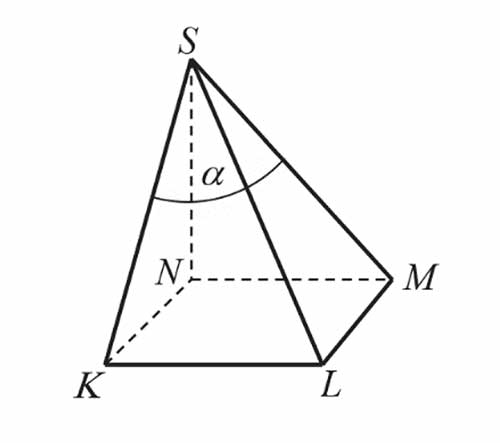
Kąt \(\alpha\), jaki tworzą krawędzie \(KS\) i \(MS\), spełnia warunek
- \(\alpha=45°\)
- \(45°<\alpha <60°\)
- \(\alpha >60°\)
- \(\alpha =60°\)

Zadanie nr 7 — maturalne.
Przekrój ostrosłupa prawidłowego trójkątnego \(ABCS\) płaszczyzną przechodzącą przez wierzchołek S i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość \(\frac{4\sqrt{3}}{3}\). Oblicz objętość tego ostrosłupa.

Zadanie nr 8 — maturalne.
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
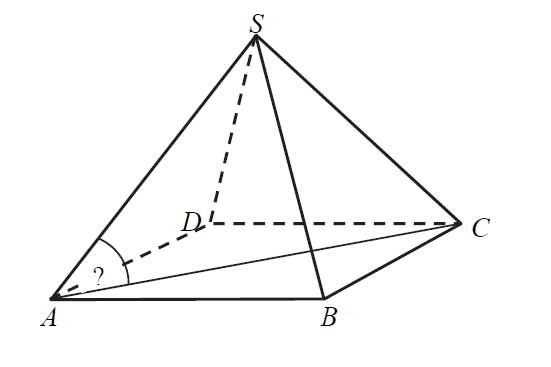
Miara kąta SAC jest równa
A. 90°
B. 75°
C. 60°
D. 45°

Zadanie nr 9 — maturalne.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt \(\alpha\) jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta \(\alpha\).
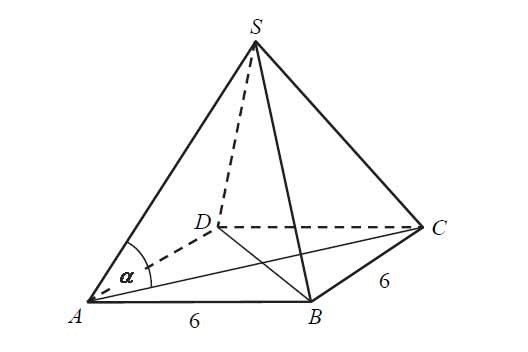

Zadanie nr 10 — maturalne.
Podstawą ostrosłupa \(ABCDS\) jest prostokąt \(ABCD\), którego boki mają długości \(|AB|=32\) i \(|BC|=18\). Ściany boczne \(ABS\) i \(CDS\) są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem \(\alpha\). Ściany boczne \(BCS\) i \(ADS\) są trójkątami przystającymi i każda z nich jest nachylona do płaszczyzny podstawy pod kątem \(\beta\) . Miary kątów \(\alpha\) i \(\beta\) spełniają warunek: \(\alpha+\beta=90°\). Oblicz pole powierzchni całkowitej tego ostrosłupa.

Zadanie nr 11 — maturalne.
Dany jest ostrosłup prawidłowy czworokątny \(ABCDS\), którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy, pod kątem którego tangens jest równy \(\sqrt{7}\). Oblicz objętość tego ostrosłupa.


Zadanie nr 12 — maturalne.
Podstawą ostrosłupa czworokątnego ABCDS jest trapez \(ABCD (AB||CD)\). Ramiona tego trapezu mają długości \(AD=10\) i \(BC=16\), a miara kąta \(ABC\) jest równa 30°. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt α, taki, że \(tg\alpha =\frac{9}{2}\). Oblicz objętość tego ostrosłupa.

Zadanie nr 13 — maturalne.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30° i ma długość równą 6 (zobacz rysunek).
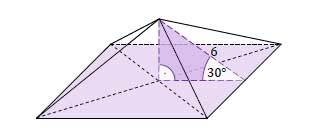
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.

Zadanie nr 14 — maturalne.
W pewnym ostrosłupie prawidłowym stosunek liczby \(W\) wszystkich wierzchołków do liczby \(K\) wszystkich krawędzi jest równy \(\frac{W}{K}=\frac{3}{5}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Podstawą tego ostrosłupa jest
A. kwadrat.
B. pięciokąt foremny.
C. sześciokąt foremny.
D. siedmiokąt foremny.
Powiązane quizy
Wybrane karty pracy
Inne zagadnienia z tej lekcji
© medianauka.pl, 2011-08-01, A-1396
Data aktualizacji artykułu: 2023-07-04



 Wielościan
Wielościan Czworościan foremny
Czworościan foremny Sześcian
Sześcian Prostopadłościan
Prostopadłościan Graniastosłup
Graniastosłup