Ciąg arytmetyczny
Co to jest ciąg arytmetyczny?
Definicja
Ciąg \((a_n)\) jest ciągiem arytmetycznym, jeżeli istnieje liczba \(r\), że dla każdego \(n\) w przypadku ciągu nieskończonego i dla każdego \(n<k\) w przypadku ciągu skończonego, k-wyrazowego oraz \(k\geq 3\) spełniony jest warunek:
Liczba \(r\) to tak zwana różnica ciągu arytmetycznego.
Mówiąc prościej, jeżeli różnica każdych dwóch kolejnych wyrazów ciągu jest stała, to mamy do czynienia z ciągiem arytmetycznym.
Przykłady ciągów arytmetycznych
Oto przykładowe ciągi arytmetyczne.
| Przykład ciągu | Różnica ciągu arytmetycznego |
|---|---|
| \((1,2,3,4,...)\) | \(r=1\) |
| \((0,-1,-2,-3,...)\) | \(r=-1\) |
| \((5,10,15,20,25)\) | \(r=5\) |
| \((-1,\sqrt{2}, 1+2\sqrt{2}, 2+3\sqrt{2}, ...)\) | \(r=1+\sqrt{2}\) |
Jak sprawdzić, czy ciąg jest arytmetyczny?
Jeżeli ciąg jest wyrażony za pomocą wzoru, to aby sprawdzić, czy dany ciąg jest arytmetyczny, należy sprawdzić różnicę dwóch kolejnych wyrazów zgodnie z definicją.
Przykład 1
Sprawdzić, czy ciąg \(a_n=n(1+\sqrt{3})-1\) jest ciągiem arytmetycznym.
Obliczamy:
\(a_{n+1}=(n+1)(1+\sqrt{3})-1=n+n\sqrt{3}+1+\sqrt{3}-1=\)
\(=n(1+\sqrt{3})+\sqrt{3}\)
Obliczamy różnicę
\(a_{n+1}-a_n=n(1+\sqrt{3})+\sqrt{3}-n(1+\sqrt{3})-1\)
\(=\sqrt{3}-1=const=r\)
Otrzymaliśmy wartość stałą (constans), a więc różnica każdych kolejnych dwóch wyrazów jest taka sama — ciąg jest ciągiem arytmetycznym.
Przykład 2
Zbadaj, czy ciąg \(a_n=\frac{1}{n}\) jest arytmetyczny.
Obliczamy
\(a_{n+1}=\frac{1}{n+1}\)
Obliczamy różnicę
\(a_{n+1}-a_n=\frac{1}{n+1}-\frac{1}{n}=\frac{n}{n(n+1)}-\frac{n+1}{n(n+1)}=\frac{-1}{n(n+1)}\neq const\)
Nie otrzymaliśmy stałej wartości, a jedynie wyrażenie zależne od liczby \(n\). Dany ciąg nie jest więc ciągiem arytmetycznym.
Wzór na n-ty wyraz ciągu arytmetycznego
Twierdzenie
Jeżeli \((a_n)\) jest ciągiem arytmetycznym, a \(r\) różnicą ciągu arytmetycznego, to dla każdego \(n\in{N_+}\) zachodzi wzór na n-ty wyraz ciągu arytmetycznego:
Zatem jeżeli znamy pierwszy wyraz ciągu i różnicę ciągu arytmetycznego, możemy obliczyć dowolny wyraz tego ciągu. Zobaczmy to na przykładzie.
Przykłady
Pierwszy wyraz ciągu arytmetycznego o różnicy \(r=5\) jest równy 3. Oblicz tysięczny wyraz ciągu arytmetycznego.
Mamy wszystkie dane, aby skorzystać ze wzoru na n-ty wyraz ciągu.
\(a_{1000}=3+(1000-1)\cdot{5}=3+999\cdot{5}=4998\)
Twierdzenie
Każdy wyraz ciągu arytmetycznego z wyjątkiem pierwszego jest średnią arytmetyczną wyrazu poprzedniego i następnego:
Suma wyrazów ciągu arytmetycznego
Wzór na sumę ciągu arytmetycznego.
Suma \(n\) kolejnych wyrazów ciągu arytmetycznego \((a_n)\) wyraża się wzorem:
Powyższe oznacza, że jeżeli mamy ciąg arytmetyczny \((a_1,a_2,a_3,...)\), to według powyższego wzoru możemy obliczyć sumę \(S_n=\underbrace{a_1+a_2+..+a_n}_{n-skladnikow}\).
Podstawiając wzór na n-ty wyraz ciągu do wzoru na sumę \(n\) kolejnych wyrazów ciągu arytmetycznego, otrzymujemy:
Przykład 1
Obliczyć sumę wszystkich liczb naturalnych od 2 do 33.
Kolejne liczby naturalne od 2 do 33 tworzą ciąg arytmetyczny \((2,4,5,...33)\). Możemy więc skorzystać ze wzoru na sumę wyrazów ciągu arytmetycznego:
\(a_1=2\)
\(n=32\) (mamy 32 wyrazy ciągu)
\(a_{32}=33\)
\(S_n=\frac{2+33}{2}\cdot{32}=560\)
Monotoniczność ciągu arytmetycznego
Ciąg arytmetyczny jest rosnący, gdy \(r>0\) i jest malejący gdy \(r<0\).
Ciąg arytmetyczny — wzory
W poniższej tabeli zamieszczono podstawowe wzory, będące podsumowaniem niniejszego artykułu.
| Nazwa | Wzór |
| ciąg arytmetyczny | \(a_{n+1}-a_n=r\) |
| n-ty wyraz ciągu arytmetycznego | \(a_n=a_1+(n-1)r\) |
| własność wyrazów ciągu arytmetycznego | \(a_n=\frac{a_{n-1}+a_{n+1}}{2}\) |
| suma wyrazów ciągu arytmetycznego | \(S_n=\frac{a_{1}+a_{n}}{2}\cdot{n}\) |
Przykładowe zadanie 1
Piąty wyraz ciągu arytmetycznego jest równy 5, a dziesiąty wyraz jest równy (-5). Wypisać trzy pierwsze wyrazy ciągu.
Korzystamy ze wzoru na n-ty wyraz ciągu arytmetycznego. Mamy więc z warunków zadania:
\(a_5=5=a_1+(5-1)r=a_1+4r\)
\(a_{10}=-5=a_1+(10-1)r=a_1+9r\)
Mamy więc układ równań:
\(\begin{cases}a_1+4r=5\\a_1+9r=-5\end{cases}\)
Odejmujemy stronami równania i otrzymujemy:
\(4r-9r=5-(-5)\)
\(-5r=10/:(-5)\)
\(r=-2\)
Podstawiamy otrzymaną wartość do pierwszego równania i otrzymujemy:
\(a_1+4\cdot(-2)=5\)
\(a_1=13\)
Obliczmy jeszcze drugi i trzeci wyraz ciągu, korzystając ze wzoru na n-ty wyraz ciągu arytmetycznego.
\(a_2=13+1\cdot(-2)=11\)
\(a_3=13+2\cdot(-2)=9\)
Odpowiedź: Pierwsze trzy wyrazy ciągu to 13, 11 i 9.
Przykładowe zadanie 2
Wyznacz wzór ogólny ciągu arytmetycznego, wiedząc, że pierwszy wyraz tego ciągu to 7, a różnica 8.
Korzystamy ze wzoru na n-ty wyraz ciągu arytmetycznego. Mamy więc z warunków zadania:
\(a_n=a_1+(n-1)r=7+(n-1)\cdot 8=7+8n-8=8n-1\)
Pytania
Jaki jest wzór na różnicę ciągu arytmetycznego?
Różnicę ciągu arytmetycznego możemy obliczyć ze wzoru \(a_{n+1}-a_n=r\). Wystarczy więc obliczyć różnicę dowolnych dwóch sąsiednich elementów ciągu.
Ile wynosi suma nieskończonego ciągu arytmetycznego?
Jeżeli dany jest ciąg arytmetyczny nieskończony, to suma wszystkich jego wyrazów jest nieskończona. Możemy obliczyć jedynie sumę skończonej liczby elementów ciągu arytmetycznego.
Zadania z rozwiązaniami

Zadanie nr 1 — maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), dane są: \(a_1=5, a_2=11\). Wtedy
A. \(a_{14}=71\)
B. \(a_{12}=71\)
C. \(a_{11}=71\)
D. \(a_{10}=71\)

Zadanie nr 2 — maturalne.
Pan Stanisław spłacił pożyczkę w wysokości 8910 zł w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 30 zł. Oblicz kwotę pierwszej raty. Zapisz obliczenia.

Zadanie nr 3 — maturalne.
W ciągu arytmetycznym \(a_n\), określonym dla każdej liczby naturalnej \(n\geq 1\), \(a_1=-1\) i \(a_4=8\). Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.

Zadanie nr 4 — maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla każdej liczby naturalnej \(n\geq 1\), \(a_5=-31\) oraz \(a_{10}=−66\). Różnica tego ciągu jest równa
A. (-7)
B. (-19,4)
C. 7
D. 19,4

Zadanie nr 5 — maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), czwarty wyraz jest równy 3, a różnica tego ciągu jest równa 5. Suma \(a_1+a_2+a_3+a_4\) jest równa
A. \(-42\)
B. \(-36\)
C. \(-18\)
D. \(6\)

Zadanie nr 6 — maturalne.
Ciąg \((a, b, c)\) jest geometryczny, ciąg \((a+1, b+5, c)\) jest malejącym ciągiem arytmetycznym oraz \(a+b+c=39\). Oblicz \(a, b, c\).

Zadanie nr 7 — maturalne.
Ciąg arytmetyczny \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\). Różnicą tego ciągu jest liczba \(r=−4\), a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu: \(a_1, a_2, a_3, a_4, a_5, a_6\) jest równa 16.
a) Oblicz pierwszy wyraz tego ciągu.
b) Oblicz liczbę \(k\), dla której \(a_{k}=−78\).

Zadanie nr 8 — maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), dane są dwa wyrazy: \(a_1= 7 i a_8=−49\). Suma ośmiu początkowych wyrazów tego ciągu jest równa
A. -168
B. -189
C. -21
D. -42

Zadanie nr 9 — maturalne.
Liczby \(a, b, c\), spełniające warunek \(3a+b+3c=77\), są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Ciąg \((a, b+1, 2c)\) jest geometryczny. Wyznacz liczby \(a, b, c\) oraz podaj wyrazy ciągu geometrycznego.

Zadanie nr 10 — maturalne.
Dwunasty wyraz ciągu arytmetycznego \((a_n)\), określonego dla \(n\geq 1\), jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.

Zadanie nr 11 — maturalne.
Dla ciągu arytmetycznego \((a_n)\), określonego dla \(n\geq 1\), jest spełniony warunek \(a_4+a_5+a_6=12\). Wtedy
A. \(a_5=4\)
B. \(a_5=3\)
C. \(a_5=6\)
D. \(a_5=5\)

Zadanie nr 12 — maturalne.
Dany jest ciąg \((a_n)\) jest określony wzorem \(a_n=\frac{(5-2n)}{6}\) dla \(n\geq 1\). Ciąg ten jest
A. arytmetyczny i jego różnica jest równa \(r=-\frac{1}{3}\).
B. arytmetyczny i jego różnica jest równa \(r=-2\).
C. geometryczny i jego iloraz jest równy \(q=-\frac{1}{3}\).
D. geometryczny i jego iloraz jest równy \(q=\frac{5}{6}\).

Zadanie nr 13 — maturalne.
Liczby \(a, b, c\) są — odpowiednio — pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa 27. Ciąg \((a−2, b, 2c+1)\) jest geometryczny. Wyznacz liczby \(a, b, c\).

Zadanie nr 14.
Znaleźć wzór na n-ty wyraz ciągu:
\((\frac{1}{2}+\frac{\sqrt{2}}{2}, 1+\sqrt{2}, \frac{3}{2}+\frac{3\sqrt{2}}{2},2+2\sqrt{2}, ...)\)

Zadanie nr 15 — maturalne.
Liczby \(2,-1,-4\) są trzema początkowymi wyrazami ciągu arytmetycznego \((a_n)\), określonego dla liczb naturalnych \(n\geq 1\). Wzór ogólny tego ciągu ma postać:
A. \(a_n=-3n+5\)
B. \(a_n=n-3\)
C. \(a_n=-n+3\)
D. \(a_n=3n-5\)

Zadanie nr 16 — maturalne.
W nieskończonym ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy \(a_1, a_3, a_k\) ciągu \((a_n)\), w podanej kolejności, tworzą nowy ciąg — trzywyrazowy ciąg geometryczny \((b_n)\). Oblicz \(k\).

Zadanie nr 17 — maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=2n^2+2n\) dla \(n\geq 1\). Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.

Zadanie nr 18 — maturalne.
Ciąg arytmetyczny \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\). Trzeci i piąty wyraz ciągu spełniają warunek \(a_3+a_5=58\). Wtedy czwarty wyraz tego ciągu jest równy
A. 28
B. 29
C. 33
D. 40

Zadanie nr 19.
Pole trójkąta prostokątnego, którego długości boków tworzą ciąg arytmetyczny, wynosi 6 cm3. Znaleźć długości wszystkich boków trójkąta.

Zadanie nr 21.
Dla jakich wartości \(x\) i \(y\) ciąg \((5, x, y, \frac{1}{5})\) jest ciągiem arytmetycznym?

Zadanie nr 22.
Znaleźć dziewiąty wyraz ciągu arytmetycznego, jeżeli wyraz piąty i siódmy jest równy odpowiednio \(7\) i \(\sqrt{7}\).

Zadanie nr 24.
Wykazać, że ciąg \(a_n=\frac{n\sqrt{2}+n}{3}\) jest ciągiem arytmetycznym.

Zadanie nr 25 — maturalne.
Czternasty wyraz ciągu arytmetycznego jest równy \(8\), a różnica tego ciągu jest równa \((-\frac{3}{2})\). Siódmy wyraz tego ciągu jest równy:
A. \(\frac{37}{2}\)
B. \(-\frac{37}{2}\)
C. \(-\frac{5}{2}\)
D. \(\frac{5}{2}\)
Powiązane materiały
 Ciąg arytmetyczny
Ciąg arytmetyczny© medianauka.pl, 2009-08-24, A-305
Data aktualizacji artykułu: 2023-05-12

 Ciąg liczbowy
Ciąg liczbowy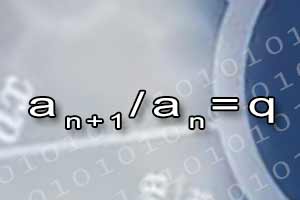 Ciąg geometryczny
Ciąg geometryczny Ciąg arytmetyczny
Ciąg arytmetyczny Wykres ciągu
Wykres ciągu Monotoniczność ciągu
Monotoniczność ciągu