Zadania — matura 2021, matematyka, poziom podstawowy
Zadania maturalne z roku 2021 z matematyki - poziom podstawowy. Są to zadania z arkuszy egzaminacyjnych wraz z rozwiązaniami.

Zadanie nr 1 - maturalne.
Liczba \(100^5\cdot (0,1)^{-6}\) jest równa
A. \(10^{13}\)
B. \(10^{16}\)
C. \(10^{-1}\)
D. \(10^{-30}\)

Zadanie nr 2 - maturalne.
Liczba \(78\) stanowi \(150%\) liczby \(c\). Wtedy liczba \(c\) jest równa
A. \(60\)
B. \(52\)
C. \(48\)
D. \(39\)

Zadanie nr 3 - maturalne.
Rozważamy przedziały liczbowe \((−\infty, 5)\) i \(\langle −1, +\infty)\). Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów?
A. \(6\)
B. \(5\)
C. \(4\)
D. \(7\)

Zadanie nr 4 - maturalne.
Suma \(2\log{\sqrt{10}}+\log{10^3}\) jest równa
A. \(2\)
B. \(3\)
C. \(4\)
D. \(5\)

Zadanie nr 5 - maturalne.
Różnica \(0,(3)-\frac{23}{33}\) jest równa
A. \(-0,(39)\)
B. \(-\frac{39}{100}\)
C. \(-0,36\)
D. \(-\frac{4}{11}\)

Zadanie nr 6 - maturalne.
Zbiorem wszystkich rozwiązań nierówności \(\frac{(2-x)}{2}-2x\geq 1\) jest przedział
A. \(\langle 0, +\infty)\)
B. \((−\infty, 0\rangle\)
C. \((−\infty, 5\rangle\)
D. \((−\infty,\frac{1}{3}\rangle\)

Zadanie nr 7 - maturalne.
Na poniższym rysunku przedstawiono wykres funkcji \(f\) określonej w zbiorze \([−6, 5]\).
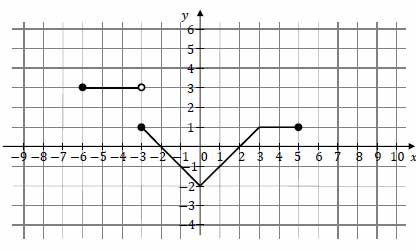
Funkcja \(g\) jest określona wzorem \(g(x)=f(x)-2\) dla \(x\in [−6, 5]\). Wskaż zdanie prawdziwe.
A. Liczba \(f(2)+g(2)\) jest równa \((−2)\).
B. Zbiory wartości funkcji \(f\) i \(g\) są równe.
C. Funkcje \(f\) i \(g\) mają te same miejsca zerowe.
D. Punkt \(P=(0,−2)\) należy do wykresów funkcji \(f\) i \(g\).

Zadanie nr 8 - maturalne.
Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań. Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
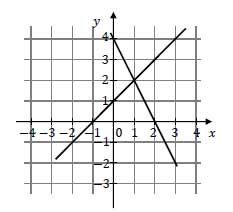
A. \(\begin{cases}y=x+1\\y=-2x+4\end{cases}\)
B. \(\begin{cases}y=x-1\\y=2x+4\end{cases}\)
C. \(\begin{cases}y=x-1\\y=2x+4\end{cases}\)
D. \(\begin{cases}y=x+1\\y=2x+4\end{cases}\)

Zadanie nr 9 - maturalne.
Na rysunku obok przedstawiono geometryczną interpretację jednego z niżej zapisanych układów
Proste o równaniach \(y=3x-5\) oraz \(y=\frac{(m-3)}{2}+\frac{9}{2}\) są równoległe, gdy
A. \(m=1\)
B. \(m=3\)
C. \(m=6\)
D. \(m=9\)

Zadanie nr 10 - maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^2}{(2x-2)}\) dla każdej liczby rzeczywistej \(x \neq 1\). Wtedy dla argumentu \(x=\sqrt{3}-1\) wartość funkcji \(f\) jest równa
A. \(\frac{1}{\sqrt{3}-1)}\)
B. \(-1\)
C. \(1\)
D. \(\frac{1}{(\sqrt{3}-2)}\)

Zadanie nr 11 - maturalne.
Do wykresu funkcji \(f\) określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=3^x-2\) należy punkt o współrzędnych
A. \((-1,-5)\)
B. \((0,-2)\)
C. \((0,-1)\)
D. \((2,4)\)

Zadanie nr 12 - maturalne.
Funkcja kwadratowa \(f\) określona wzorem \(f(x)=-2(x+1)(x-3)\) jest malejąca w przedziale
A. \([1, +\infty)\)
B. \((−\infty, 1]\)
C. \((−\infty, −8]\)
D. \([−8, +\infty)\)

Zadanie nr 13 - maturalne.
Trzywyrazowy ciąg \((15, 3x, \frac{5}{3})\) jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że:
A. \(x=\frac{3}{5}\)
B. \(x=\frac{4}{5}\)
C. \(x=1\)
D. \(x=\frac{5}{3}\)

Zadanie nr 14 - maturalne.
Ciąg \((b_n)\) jest określony wzorem \(b_n=3n^2-25n\) dla każdej liczby naturalnej \(n\geq 1\). Liczba niedodatnich wyrazów ciągu \((b_n)\) jest równa
A. 14
B. 13
C. 9
D. 8

Zadanie nr 15 - maturalne.
Ciąg arytmetyczny \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\). Trzeci i piąty wyraz ciągu spełniają warunek \(a_3+a_5=58\). Wtedy czwarty wyraz tego ciągu jest równy
A. 28
B. 29
C. 33
D. 40

Zadanie nr 16 - maturalne.
Dla każdego kąta ostrego α iloczyn \(\frac{cos\alpha}{1-\sin^2\alpha}\cdot \frac{1-cos^2\alpha}{sin\alpha}\) jest równy
A. \(\sin{\alpha}\)
B. \(tg\alpha\)
C. \(\cos{\alpha}\)
D. \(\sin^2{\alpha}\)

Zadanie nr 17 - maturalne.
Prosta \(k\) jest styczna w punkcie \(A\) do okręgu o środku \(O\). Punkt \(B\) leży na tym okręgu i miara kąta \(AOB\) jest równa 80°. Przez punkty \(O\) i \(B\) poprowadzono prostą, która przecina prostą \(k\) w punkcie \(C\) (zobacz rysunek).
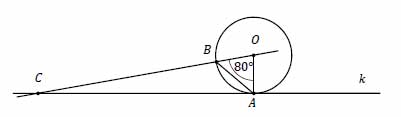
A. 10°
B. 30°
C. 40°
D. 50°

Zadanie nr 18 - maturalne.
Przyprostokątna \(AC\) trójkąta prostokątnego ABC ma długość 8 oraz \(tg\alpha=\frac{2}{5}\) (zobacz rysunek).
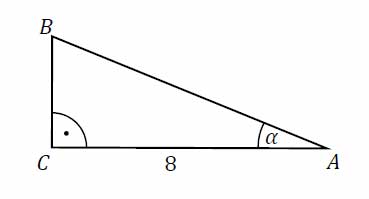
Pole tego trójkąta jest równe
A. \(12\)
B. \(\frac{37}{3}\)
C. \(\frac{62}{5}\)
D. \(\frac{64}{5}\)

Zadanie nr 19 - maturalne.
Pole pewnego trójkąta równobocznego jest równe \(\frac{4\sqrt{3}}{9}\). Obwód tego trójkąta jest równy
A. 4
B. 2
C. \(\frac{4}{3}\)
D. 2/3

Zadanie nr 20 - maturalne.
W trójkącie \(ABC\) bok \(BC\) ma długość 13, a wysokość \(CD\) tego trójkąta dzieli bok \(AB\) na odcinki o długościach \(|AD|=3\) i \(|BD|=12\) (zobacz rysunek obok). Długość boku \(AC\) jest równa
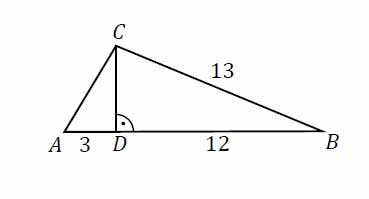
A. \(\sqrt{34}\)
B. \(\frac{13}{4}\)
C. \(2\sqrt{14}\)
D. \(3\sqrt{45}\)

Zadanie nr 21 - maturalne.
Punkty \(A, B, C\) i \(D\) leżą na okręgu o środku S. Miary kątów \(SBC, BCD, CDA\) są równe odpowiednio: \(|\angle SBC|=60°, |\angle BCD|=110°, |\angle CDA|=90°\) (zobacz rysunek).
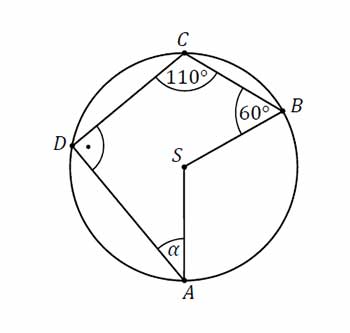
Wynika stąd, że miara \(\alpha\); kąta \(DAS\) jest równa
A. 25°
B. 30°
C. 35°
D. 40°

Zadanie nr 22 - maturalne.
W równoległoboku \(ABCD\), przedstawionym na rysunku, kąt α ma miarę 70°.
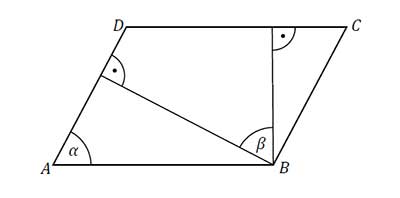
Wtedy kąt β ma miarę
A. 80°
B. 70°
C. 60°
D. 50°

Zadanie nr 23 - maturalne.
W każdym n-kącie wypukłym (n≥ 3) liczba przekątnych jest równa n(n-3)/2. Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
A. siedmiokąt.
B. dziesięciokąt.
C. dwunastokąt.
D. piętnastokąt.

Zadanie nr 24 - maturalne.
Pole figury \(F_1\) złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury \(F_2\) złożonej z dwóch stycznych zewnętrznie kół o promieniach długości \(r\) (zobacz rysunek).
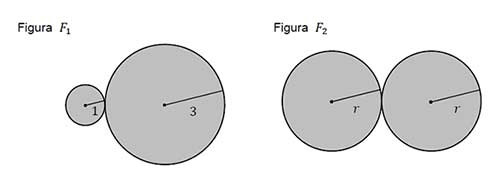
Długość \(r\) promienia jest równa
A. \(\sqrt{3}\)
B. \(2\)
C. \(\sqrt{5}\)
D. \(3\)

Zadanie nr 25 - maturalne.
Punkt \(A=(3,−5)\) jest wierzchołkiem kwadratu \(ABCD\), a punkt \(M=(1,3)\) jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu \(ABCD\) jest równe
A. \(68\)
B. \(136\)
C. \(2\sqrt{34}\)
D. \(8\sqrt{34}\)

Zadanie nr 26 - maturalne.
Z wierzchołków sześcianu \(ABCDEFGH\) losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześcianu \(ABCDEFGH\), jest równe
A. \(\frac{1}{7}\)
B. \(\frac{4}{7}\)
C. \(\frac{1}{14}\)
D. \(\frac{3}{7}\)

Zadanie nr 27 - maturalne.
Wszystkich liczb naturalnych trzycyfrowych, większych od 700, w których każda cyfra należy do zbioru {1, 2, 3, 7, 8, 9} i żadna cyfra się nie powtarza, jest
A. 108
B. 60
C. 40
D. 299

Zadanie nr 28 - maturalne.
Sześciowyrazowy ciąg liczbowy \((1, 2, 2x, x + 2, 5, 6)\) jest niemalejący. Mediana wyrazów tego ciągu jest równa \(4\). Wynika stąd, że
A. \(x=1\)
B. \(x=\frac{3}{2}\)
C. \(x=2\)
D. \(x=\frac{8}{3}\)

Zadanie nr 30 - maturalne.
Wykaż, że dla każdych trzech dodatnich liczb \(a,b\) i \(c\) takich, że \(a<b\), spełniona jest nierówność \(\frac{a}{b}<\frac{(a+c)}{(b+c)}\).

Zadanie nr 31 - maturalne.
Funkcja liniowa \(f\) przyjmuje wartość \(2\) dla argumentu \(0\), a ponadto \(f(4)-f(2)=6\). Wyznacz wzór funkcji \(f\).

Zadanie nr 33 - maturalne.
Trójkąt równoboczny \(ABC\) ma pole równe \(9\sqrt{3}\). Prosta równoległa do boku \(BC\) przecina boki \(AB\) i \(AC\) — odpowiednio — w punktach \(K\) i \(L\). Trójkąty \(ABC\) i \(AKL\) są podobne, a stosunek długości boków tych trójkątów jest równy \(\frac{3}{2}\). Oblicz długość boku trójkąta \(AKL\).

Zadanie nr 34 - maturalne.
Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia A polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.

Zadanie nr 35 - maturalne.
Punkty \(A=(−20, 12)\) i \(B=(7, 3)\) są wierzchołkami trójkąta równoramiennego ABC, w którym \(|AC|=|BC|\). Wierzchołek \(C\) leży na osi \(Oy\) układu współrzędnych. Oblicz współrzędne wierzchołka \(C\) oraz obwód tego trójkąta.
Liczba odnalezionych zadań w zbiorze: 35.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.


Źródło: Centralna Komisja Egzaminacyjna







