Pochodna funkcji
Pochodna funkcji to jedno z najważniejszych pojęć matematycznych. Jest to narzędzie, z którego matematycy korzystają bardzo często nie tylko w analizie matematycznej. Bez rachunku pochodnych nie ma podstaw fizyki, chemii i innych dziedzin nauki. W tym artykule pochodną funkcji wprowadzimy w nieco inny sposób, niż to czynią autorzy popularnych podręczników.
Wprowadzenie
Zaczniemy od pojęcia prędkości. Jeżeli chcemy zmierzyć, z jaką prędkością jedzie samochód, wystarczy zmierzyć położenie \(x_1\) samochodu w chwili \(t_1\) i po chwili znów położenie \(x_2\) samochodu w chwili \(t_2\). W ten sposób wiemy, że samochód przemieścił się o \(x=x_2-x_1\) w czasie \(∆t=t_@-t_1\). Prędkość średnią obliczymy, dzieląc jedną wielkość przez drugą: \(v_{sr}=\frac{\Delta{x}}{\Delta{t}}\).
Jest to prosta metoda wyznaczania prędkości, ale mało dokładna, bo w czasie \(\Delta t\) (np. między pierwszą a drugą godziną ruchu) położenie ciała w układzie odniesienia może się zmieniać w różny i znaczący sposób (np. w pierwszych minutach ruchu ciało może się nie przemieszczać wcale, potem szybko, a później jeszcze inaczej). Dlatego właśnie jest to prędkość średnia. Aby dokładniej mierzyć prędkość, można mierzyć ją częściej i w krótszych odstępach czasu. Dalej jest to jednak wartość średnia. Jak zatem obliczyć prędkość w danej chwili? Jak obliczyć przemieszczenie obiektu w konkretnej chwili? Od razu widać, że brakuje nam aparatu matematycznego, aby to zrobić.
W tym momencie przydaje się pojęcie pochodnej. Znamy pojęcie granicy funkcji i wykorzystajmy je tutaj. A gdyby tak brać pod uwagę bardzo małe odcinki czasu, tak małe, że nieskończenie bliskie zeru? Pamiętajmy, że w mianownik musi być różny od zera. Możemy jednak obliczyć granicę \(\displaystyle\lim_{\Delta t\to 0}{\frac{\Delta x}{\Delta t}}\), otrzymując dokładną wartość prędkości w danej chwili pomiaru ruchu. Jeżeli wiemy, że położenie obiektu w układzie odniesienia jest funkcją czasu, to bez problemu będziemy w stanie obliczyć prędkość chwilową w dowolnej chwili. Wybiegając nieco do przodu, stwierdzamy, że prędkość chwilowa jest to pochodna położenia względem czasu i zapisujemy to następująco: \(v_{sr}=\frac{dx}{dt}\).
Jest to tylko jeden z prostych przykładów przydatności pochodnej funkcji i pokazuje praktyczny aspekt jej stosowania w fizyce. Zdefiniujmy jednak najpierw pochodną, zanim zaczniemy ją stosować w różnych innych przypadkach.
Iloraz różnicowy
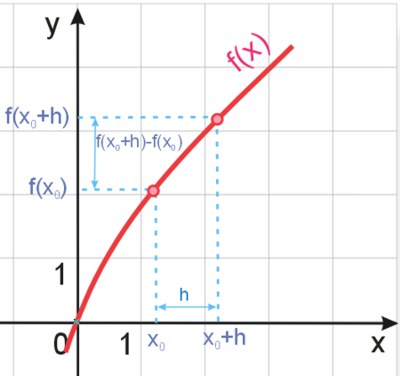
Niech \(f(x)\) oznacza dowolną funkcję, określoną w pewnym otoczeniu \(U\) punktu \(x_0\).
Zaznaczamy na osi \(Ox\) pewien przyrost argumentów funkcji oraz na osi \(Oy\) odpowiadający mu przyrost wartości funkcji. Przyrost argumentów funkcji oznaczamy przez \(h\). Zauważ, że \((x_0+h)-x_0=h\). Niech \(h\) jest liczbą różną od zera i \(x_0+h\in U\).
Iloraz \(\frac{f(x_0+h)-f(x_0)}{h}\) nazywamy ilorazem różnicowym funkcji \(f(x)\) w punkcie \(x_0\) dla przyrostu \(h\).
Zauważ, że w omawianym przykładzie z prędkością chwilową i średnią również mamy do czynienia z ilorazem różnicowym, gdyż iloraz \(\frac{\Delta x}{\Delta t}\) można zapisać jako:
\(v_{sr}=\frac{x_2-x_1}{t_2-t_1}=\frac{x(t_1+\Delta t)-x(t_1)}{\Delta t}=\frac{x(t_1+h)-f(t_1)}{h}, \ h=\Delta t"\)
Możemy więc zapamiętać, że:
\(\frac{f(x_0+h)-f(x_0)}{h}=\frac{\Delta y}{\Delta x}=\frac{przyrost \ wartości \ funkcji}{przyrost \ argumentu}\)
Pochodna funkcji w punkcie
Definicja
Jeśli iloraz różnicowy ma w punkcie \(x_0\) granicę, gdy \(h\) dąży do zera, to tę granicę nazywamy pochodną funkcji w punkcie \(x_0\) i oznaczamy \(f'(x_0)\).
Jeżeli funkcja \(f(x)\) ma pochodną w punkcie \(x_0\), to mówimy, że jest różniczkowalna w tym punkcie.
Przykład
Obliczymy pochodną funkcji \(f(x)=2x+1\) w punkcie \(x_0=1\).
\(f(x_0)=f(1)=2\cdot 1+1=3\)
\( f(x_0+h)=f(1+h)=2(1+h)+1=2+2h+1=2h+3\)
\( f'(x_0)=f'(1)=\displaystyle\lim_{h\to 0}{\frac{f(x_0+h)-f(x_0)}{h}}=\lim_{h\to 0}{\frac{2h+3-3}{h}}=\lim_{h\to 0}{\frac{2h}{h}}=2\)
Interpretacja geometryczna pochodnej
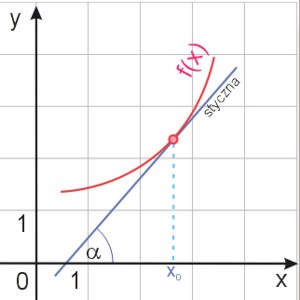
Pochodna \(f'(x_0)\) jest równa tangensowi kąta nachylenia stycznej do krzywej o równaniu \(y=f(x)\) w punkcie o odciętej \(x_0\) do osi \(Ox\).
Zostało to zilustrowane na zamieszczonym obok rysunku.
Możemy też stwierdzić, że pochodna funkcji w punkcie jest równa współczynnikowi kierunkowemu stycznej do krzywej \(y=f(x)\) w punkcie o odciętej \(x_0\).
Różniczkowalność a ciągłość funkcji
Twierdzenie
Ciągłość funkcji jest warunkiem koniecznym dla istnienia pochodnej, ale nie jest warunkiem wystarczającym. Twierdzenie odwrotne do powyższego nie jest prawdziwe, to znaczy, że jeśli funkcja jest ciągła w punkcie \(x_0\), to nie znaczy, że jest różniczkowalna w tym punkcie.
Jeżeli funkcja nie jest ciągła w danym punkcie, to nie ma w tym punkcie pochodnej.
To, czy funkcja jest różniczkowalna w danym punkcie, można poznać także na podstawie jej wykresu.
Funkcja nie jest różniczkowalna w punktach, w których wykres tworzy „ostrza”. Na poniższej ilustracji pokazano wykresy funkcji, które nie są różniczkowalne w punkcie \(x_0\).
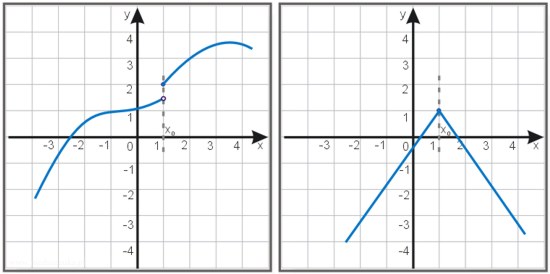
Przykładem funkcji, która w punkcie \(x_0\) jest ciągła, a nie jest różniczkowalna (nie ma pochodnej w tym punkcie) jest funkcja \(f(x)=|x|\).
Obliczanie pochodnych
Wyżej omówiliśmy pojęcie pochodnej w punkcie, jej interpretację geometryczną. Pora zająć się metodami wyznaczania pochodnej. Najpierw jednak określimy pochodną jako funkcję.
Pochodna jako funkcja
Jeżeli funkcja \(f(x)\) ma pochodną w każdym punkcie \(x\) pewnego przedziału, to określona jest w tym przedziale funkcja \(x\to y=f'(x)\).
Mówiąc inaczej, jeżeli każdemu punktowi z dziedziny funkcji \(f(x)\) przyporządkujemy pochodną w tym punkcie (o ile istnieje), to określimy w ten sposób funkcję, którą nazywamy pochodną funkcji \(f(x)\) i oznaczamy przez \(f '(x)\).
Przykład
Dla przykładu obliczymy pochodną funkcji \(f(x)=2x+1\).
\(f(x)=2x+1\)
\(f(x+h)=2(x+h)+1=2x+2h+1\)
\(f'(x)=\displaystyle\lim_{h\to 0}{\frac{f(x+h)-f(x)}{h}}=\lim_{h\to 0}{\frac{2x+2h+1-(2x+1)}{h}}=\lim_{h\to 0}{\frac{2h}{h}}=2\)
Jak widać, sposób postępowania przy obliczaniu pochodnej funkcji jest analogiczny do obliczania pochodnej funkcji w punkcie.
Pochodne funkcji elementarnych
W poniższej tabeli zostały zawarte podstawowe wzory na obliczenie pochodnych funkcji elementarnych.
Nauczenie się ich na pamięć jest bardzo ważne w sprawnym posługiwaniu się rachunkiem pochodnych.

Tablica pochodnych
Poniższa tablica prezentuje podstawowe pochodne. Wzory te są bardzo często wykorzystywane w matematyce i fizyce. Warto się ich nauczyć na pamięć.
| Funkcja | Pochodna | Uwagi |
|---|---|---|
| \(c\) | \(0\) | \(x\in \mathbb{R}\) |
| \(x^n\) | \(nx^{n-1}\) | \(x\in R, \ gdy \ n\in \mathbb{N}\) \( x\in R_+, \ gdy \ n\in \mathbb{W}\) |
| \(\sqrt{x}\) | \(\frac{1}{2\sqrt{x}}\) | \(x\in \mathbb{R}_+\) |
| \(\frac{1}{x}\) | \(-\frac{1}{x^2}\) | \(x\neq 0\) |
| \(\sin{x}\) | \(\cos{x}\) | \(x\in R\) |
| \(\cos{x}\) | \(-\sin{x}\) | \(x\in \mathbb{R}\) |
| \(tg{x}\) | \(\frac{1}{\cos^2{x}}\) | \(\cos{x}\neq 0\) |
| \(ctg{x}\) | \(-\frac{1}{\sin^2{x}}\) | \(\sin{x}\neq 0\) |
| \(a^x\) | \(a^x\cdot \ln{a}\) | \(a\in \mathbb{R}_+\) |
| \(e^x\) | \(e^x\) | |
| \(\ln{x}\) | \(\frac{1}{x}\) | \(x>0\) |
| \(\log_{a}{x}\) | \(\frac{1}{x\ln{a}}\) | \(x>0, \ a>0, \ a\neq 1\) |
| \(\arcsin{x}\) | \(\frac{1}{\sqrt{1-x^2}}\) | \(|x|<1\) |
| \(\arccos{x}\) | \(-\frac{1}{\sqrt{1-x^2}}\) | \(|x|<1\) |
| \(arctg{x}\) | \(\frac{1}{1+x^2}\) | |
| \(arcctg{x}\) | \(\frac{-1}{1+x^2}\) |
Przykłady
Dla przykładu obliczymy na podstawie powyższych wzorów kilka pochodnych.
- \(y=5,\ y'=0\)
- \(f(x)=x^2\ f'(x)=2x^{2-1}=2x^1=2x\)
- \(f(x)=x=x^1,\ f'(x)=1\cdot x^{1-1}=x^0=1\)
- \(y=x^{10},\ y'=10x^9\)
Pochodna sumy, iloczynu i ilorazu
W poniższej tabeli zostały zawarte podstawowe wzory na obliczenie pochodnej sumy, różnicy iloczynu i ilorazu funkcji.
| Nazwa | WZÓR |
|---|---|
| pochodna sumy | \([f(x)+g(x)]'=f'(x)+g'(x)\) |
| pochodna różnicy | \([f(x)-g(x)]'=f'(x)-g'(x)\) |
| pochodna iloczynu | \([f(x)\cdot g(x)]'=f'(x)g(x)+f(x)g'(x)\) |
| pochodna ilorazu | \([\frac{f(x)}{g(x)}]'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\) |
| mnożenie przez stałą | \([c\cdot f(x)]'=c\cdot f'(x)\) |
Przykłady
Dla przykładu obliczymy na podstawie powyższych wzorów kilka pochodnych.
1) Pochodna sumy i różnicy funkcji.
\(f(x)=5x+2\)
\(f'(x)=(5x)'+(2)'=5+0=5\)
\(g(x)=x^2-\frac{1}{x}\)
\(g'(x)=(x^2)'-(\frac{1}{x})'=2x-(-\frac{1}{x^2})=2x+\frac{1}{x^2}\)
2) Pochodna iloczynu funkcji.
\(f(x)=5x\sqrt{x}\)
\(f'(x)=(5x)'\cdot \sqrt{x}+5x\cdot (\sqrt{x})'=5\sqrt{x}+5x\cdot \frac{1}{2\sqrt{x}}\)
3) Pochodna ilorazu funkcji.
\(f(x)=\frac{x+1}{x^2}\)
\(f'(x)=\frac{(x+1)'\cdot x^2-(x+1)\cdot (x^2)'}{(x^2)^2}=\frac{x^2-2x(x+1)}{x^4}=\frac{x^2-2x^2-2x}{x^4}=\\=\frac{-x^2-2x}{x^4}=\frac{x(-x-2)}{x^4}=\frac{-x-2}{x^3}\)
4) Pochodna iloczynu funkcji i stałej.
\(f(x)=5x^9\)
\(f'(x)=5\cdot(x^9)'=5\cdot 9x^8=45x^8\)
Pytania
Jakie zastosowanie mają pochodne?
Pochodne są bardzo istotną częścią języka matematycznego, którym posługuje się praktycznie cała fizyka i nauki techniczne. Większość wzorów w fizyce wykorzystuje właśnie pochodne. Pochodne pojawiają się także w naukach przyrodniczych i ekonomicznych. W matematyce bez pochodnych praktycznie nie ma analizy funkcji. Zadania z treścią, które omawiamy w dalszej części lekcji, pokazują, że pochodne mają także zastosowanie w życiu codziennym.
Zadania z rozwiązaniami

Zadanie nr 1.
Obliczyć pochodną funkcji \(f(x)=-x^2+x-1\) w punkcie \(x_0=-1\).

Zadanie nr 3.
Obliczyć pochodną funkcji \(f(x)=\frac{1}{x+1}\) w punkcie \(x_0=0\).

Zadanie nr 5.
Obliczyć pochodną funkcji \(f(x)=\begin{cases} x^2 \ dla \ x\geq 0 \\ -2x^2 \ dla \ x<0 \end{cases}\) w punkcie \(x_0=0\).

Zadanie nr 7.
Obliczyć pochodną funkcji
\(a) f(x)=-\frac{1}{2}\)
\(b) g(x)=x^{17}\)
\(c) h(x)=x^{\frac{1}{3}}\)
\( d) i(x)=x\)
\( e) j(x)=\sqrt{2}\)

Zadanie nr 8.
Obliczyć pochodną funkcji:
\(a) f(x)=-x+5\)
\(b) g(x)=-5x^2+2\sqrt{x}\)
\( c) h(x)=\sin{x}+2\cos{x}\)
\( d) i(x)=-\frac{1}{x}-tgx\)
\( e) j(x)=3x^3-2x^2+x-1\)

Zadanie nr 9.
Obliczyć pochodną funkcji:
\(a) f(x)=x\sin{x}\)
\(b) g(x)=\sin^2{x}\)
\(c) h(x)=x\sqrt{x}\)

Zadanie nr 10.
Obliczyć pochodną funkcji:
a) \(f(x)=\frac{\sin{x}}{x}\)
b) \(f(x)=\frac{2x+1}{3x-1}\)
c) \(f(x)=\frac{\sin{x}}{\cos{x}}\)

Zadanie nr 11.
Obliczyć pochodną funkcji:
a) \(f(x)=\frac{\sqrt{x}}{x}\)
b) \(f(x)=\frac{5x^3-x+1}{x^2-1}\)
c) \(f(x)=\frac{5x^4-3x^2}{2x^3-1}\)

Zadanie nr 12.
Obliczyć pochodną funkcji \(f(x)=\frac{\sqrt[5]{x}}{10x^8}\).

Zadanie nr 13 — maturalne.
Funkcja \(f(x)=\frac{3x-1}{x^2+4}\) jest określona dla każdej liczby rzeczywistej \(x\). Pochodna tej funkcji jest określona wzorem:
A. \(f'(x)=\frac{-3x^2+2x+12}{(x^2+4)^2}\)
B. \(f'(x)=\frac{-9x^2+2x-12}{(x^2+4)^2}\)
C. \(f'(x)=\frac{3x^2-2x-12}{(x^2+4)^2}\)
D. \(f'(x)=\frac{9x^2-2x+12}{(x^2+4)^2}\)

Zadanie nr 14 — maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^3-8}{x-2}\) dla każdej liczby rzeczywistej \(x\neq 2\). Wartość pochodnej tej funkcji dla argumentu \(x=\frac{1}{2}\) jest równa
A. \(\frac{3}{4}\)
B. \(\frac{9}{4}\)
C. 3
D. \(\frac{54}{8}\)
Powiązane materiały
 Pochodne
Pochodne© medianauka.pl, 2010-09-03, A-885
Data aktualizacji artykułu: 2023-05-15

 Pochodna funkcji złożonej
Pochodna funkcji złożonej Pochodna drugiego rzędu i dalsze pochodne
Pochodna drugiego rzędu i dalsze pochodne Pochodne cząstkowe
Pochodne cząstkowe Pochodna funkcji
Pochodna funkcji Pochodna w zadaniach z treścią
Pochodna w zadaniach z treścią Pochodna a monotoniczność funkcji
Pochodna a monotoniczność funkcji Pochodna funkcji a ekstremum
Pochodna funkcji a ekstremum Przebieg zmienności funkcji
Przebieg zmienności funkcji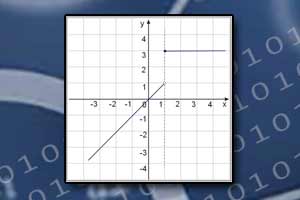 Ciągłość funkcji
Ciągłość funkcji Pochodne funkcji elementarnych — quiz
Pochodne funkcji elementarnych — quiz