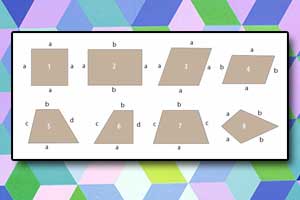
Zadania — czworokąty
Znajdziesz tutaj zadania z działu o czworokątach, w tym takich figur i zagadnień jak kwadraty, prostokąty, romby, trapezy, równoległoboki, pola powierzchni i własności tych figur. To zadania z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 1.
Dany jest trójkąt \(ABC\) o bokach długości: \(|AB|=6, |BC|=4, |AC|=5\). Punkt \(M\) jest środkiem boku \(AC\), punkt \(N\) — środkiem boku \(BC\). Obliczyć obwód trapezu \(ABNM\).
Zadanie nr 3.
Na kole o promieniu \(r=5\) opisano kwadrat. Oblicz jego pole.
Zadanie nr 4.
Oblicz pole kwadratu \(ABCD\), jeżeli wiadomo, że \(A=(3,0), B=(4,2), C=(2,3), D=(1,1)\).
Zadanie nr 5.
Na obszarze w kształcie kwadratu o powierzchni 1 ha organizowany jest koncert. Przyjmuje się, że na dany obszar można wpuścić tyle ludzi, że na każdego przypada 1 m2 wolnej powierzchni. Jaki przychód z koncertu będą mieli organizatorzy, jeśli zostaną sprzedane wszystkie bilety, których cena wynosi 30 zł?
Zadanie nr 6.
W jakiej odległości znajdują się od siebie każde odpowiadające sobie wierzchołki dwóch kwadratów o wspólnym środku, jeżeli jeden z kwadratów ma pole dwa razy mniejsze od drugiego i bok większego kwadratu ma długość równą 20?
Zadanie nr 7.
Środki kwadratu o boku \(a=10\) połączono tak, że powstał w środku mniejszy kwadrat. Oblicz jego pole.
Zadanie nr 8.
Ile będzie kosztował zakup kafli podłogowych dla przedstawionego na rysunku planu łazienki, jeżeli na ścinki i uszkodzenia założymy 5% rezerwy, zaokrąglając liczbę metrów kwadratowych w górę, a metr kwadratowy kafelek kosztuje 45 zł?
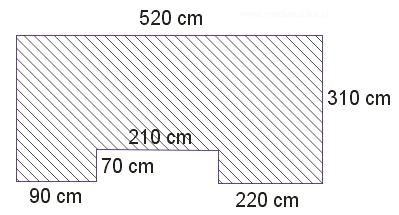
Zadanie nr 9.
Długość jednego z boków prostokąta jest dwa razy większa od długości drugiego boku prostokąta. Przekątna prostokąta ma długość równą 3. Oblicz długości boków.
Zadanie nr 10.
Obwód prostokąta jest równy 14, a jego pole jest równe 12. Obliczyć długości boków tego prostokąta.
Zadanie nr 11.
Przekątna kwadratu pokrywa się z ramieniem trójkąta równoramiennego o polu równym 16. Oblicz pole kwadratu.
Zadanie nr 12.
Obwód prostokąta jest równy 10, długość jego przekątnej \(\sqrt{13}\). Oblicz pole tego prostokąta.
Zadanie nr 13.
Oblicz pole prostokąta, którego przekątne każda o długości 10 tworzą ze sobą kąt 30°.
Zadanie nr 14.
Pole prostokąta, którego przekątne tworzą ze sobą kąt 30°, jest równe 16. Oblicz długość przekątnej tego prostokąta.
Zadanie nr 15.
Długość jednej z podstaw trapezu jest dwa razy większa od długości drugiej podstawy. Długość środkowej równoległej do podstaw jest równa 3. Obliczyć długości podstaw tego trapezu.
Zadanie nr 16.
W trapezie prostokątnym długość podstaw jest równa odpowiednio 3 i 6, a długość krótszego z ramion 2. Oblicz długość dłuższego ramienia trapezu.
Zadanie nr 17.
Długości przekątnych rombu są równe 6 i 8. Oblicz długość boku tego rombu.
Zadanie nr 18.
Oblicz pole trapezu równoramiennego, którego wysokość ma długość 2, krótsza podstawa 4, a ramię ma długość 3.
Zadanie nr 19.
Jedna z wysokości w równoległoboku o polu 10 ma długość 2, druga z wysokości ma długość 4. Oblicz obwód tego równoległoboku.
Zadanie nr 20.
Kąt między dwoma bokami równoległoboku o długościach 5 cm i 6 cm ma miarę równą 30°. Oblicz pole tego równoległoboku.
Zadanie nr 21.
Obliczyć pole równoległoboku \(ABCD\), jeżeli wiadomo, że \(A=(1,1), B=(5,1), C=(7,3), D=(3,3)\).
Zadanie nr 22.
Długość krótszego boku równoległoboku oraz jednej z jego przekątnych jest równa. Oblicz pole powierzchni tego równoległoboku, jeżeli wiadomo, że drugi z boków jest razy dłuższy od pierwszego.
Zadanie nr 23.
Przekątna kwadratu o boku 1 oraz połowa drugiej przekątnej kwadratu stanowią przekątne rombu. Oblicz jego pole i obwód.
Zadanie nr 24.
Oblicz pole rombu \(ABCD\), jeżeli wiadomo, że \(A=(2,0), B=(3,2), C=(2,4), D=(1,2)\).
Zadanie nr 25.
Dany jest romb o boku \(a=\sqrt{2}\). Kąt wewnętrzny ma miarę 60°. Obliczyć pole powierzchni tego rombu.
Zadanie nr 26.
Wysokość rombu o polu 3 ma wartość \(\frac{3}{2}\). Oblicz obwód tego rombu.
Zadanie nr 27.
Z dwóch listewek o długości 30 cm i 1,2 m oraz kawałka materiału zbudowano latawiec w kształcie deltoidu tak, że listewki tworzą jego przekątne. Jakie jest pole powierzchni użytego materiału?

Zadanie nr 28 - maturalne.
Punkty \(A=(30,32)\) i \(B=(0,8)\) są sąsiednimi wierzchołkami czworokąta \(ABCD \) wpisanego w okrąg. Prosta o równaniu \(x-y+2=0\) jest jedyną osią symetrii tego czworokąta i zawiera przekątną \(AC\). Oblicz współrzędne wierzchołków \(C\) i \(D\) tego czworokąta.

Zadanie nr 29 - maturalne.
Pole rombu o obwodzie 8 jest równe 1. Kąt ostry tego rombu ma miarę \(\alpha\). Wtedy:
A. \(14°<\alpha< 15°\)
B. \(29°<\alpha< 30°\)
C. \(60°<\alpha< 61°\)
D. \(75°<\alpha< 76°\)

Zadanie nr 30 - maturalne.
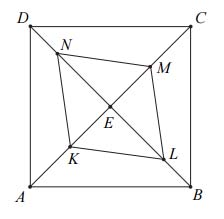
Dany jest kwadrat \(ABCD\). Przekątne \(AC\) i \(BD\) przecinają się w punkcie \(E\). Punkty \(K\) i \(M\) są środkami odcinków – odpowiednio – \(AE\) i \(EC\). Punkty \(L\) i \(N\) leżą na przekątnej \(BD\) tak, że \(|BL|=\frac{1}{3}|BE|\) i \(|DN|=\frac{1}{3}|DE|\) (zobacz rysunek). Wykaż, że stosunek pola czworokąta \(KLMN\) do pola kwadratu \(ABCD\) jest równy 1:3.

Zadanie nr 31 - maturalne.
Punkt \(C=(0,2)\) jest wierzchołkiem trapezu \(ABCD\), którego podstawa AB jest zawarta w prostej o równaniu \(y=2x-4\). Wskaż równanie prostej zawierającej podstawę \(CD\).
A. \(y=\frac{1}{2}x+2\)
B. \(y=-2x+2\)
C. \(y=-\frac{1}{2}x+2\)
D. \(y=2x+2\)

Zadanie nr 32 - maturalne.
Wysokość trapezu równoramiennego o kącie ostrym 60° i ramieniu długości \(2\sqrt{3}\) jest równa:
A. \(\sqrt{3}\)
B. \(3\)
C. \(2\sqrt(3)\)
D. \(2\)

Zadanie nr 33 - maturalne.
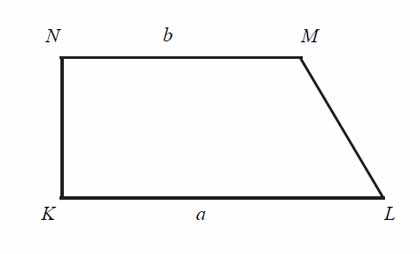
Dany jest trapez prostokątny \(KLMN\), którego podstawy mają długości \(KL=a, MN=b,
a>b\). Kąt \(KLM\) ma miarę 60°. Długość ramienia \(LM\) tego trapezu jest równa:
A. \(a-b\)
B. \(2(a-b)\)
C. \(a+\frac{b}{2}\)
D. \((a+b)/2\)

Zadanie nr 34 - maturalne.
Dany jest romb o boku długości 4 i kącie rozwartym 150°. Pole tego rombu jest równe
A. 8
B. 12
C. \(8\sqrt{3}\)
D. 16

Zadanie nr 35 - maturalne.
W trapezie prostokątnym \(ABCD\) dłuższa podstawa \(AB\) ma długość 8. Przekątna AC tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze (zobacz rysunek). Oblicz długość przekątnej \(BD\) tego trapezu.
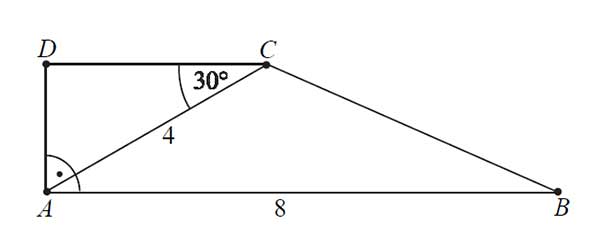

Zadanie nr 36 - maturalne.
Pole prostokąta ABCD jest równe 90. Na bokach \(AB\) i \(CD\) wybrano — odpowiednio — punkty \(P\) i \(R\), takie, że \(\frac{|AP|}{|PB|}=\frac{|CR|}{|RD|}=\frac{3}{2}\) (zobacz rysunek).
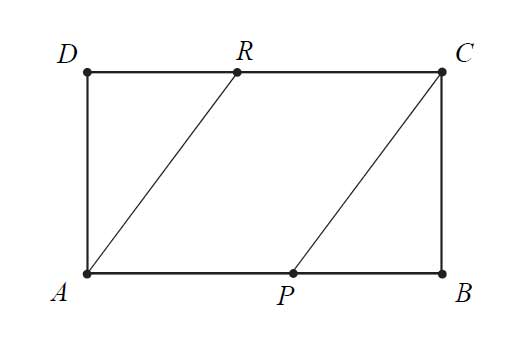
Pole czworokąta \(APCR\) jest równe
A. 36
B. 40
C. 54
D. 60

Zadanie nr 37 - maturalne.
Dany jest kwadrat \(ABCD\), w którym \(A=(5, -\frac{5}{3})\). Przekątna \(BD\) tego kwadratu jest zawarta w prostej o równaniu \(y =\frac{4}{3}x\). Oblicz współrzędne punktu przecięcia przekątnych \(AC\) i \(BD\) oraz pole kwadratu \(ABCD\).

Zadanie nr 38 - maturalne.
Podstawą ostrosłupa czworokątnego ABCDS jest trapez \(ABCD (AB||CD)\). Ramiona tego trapezu mają długości \(AD=10\) i \(BC=16\), a miara kąta \(ABC\) jest równa 30°. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt α, taki, że \(tg\alpha =\frac{9}{2}\). Oblicz objętość tego ostrosłupa.

Zadanie nr 39 - maturalne.
W równoległoboku \(ABCD\), przedstawionym na rysunku, kąt α ma miarę 70°.
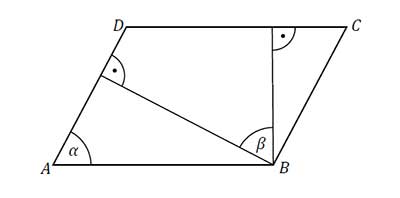
Wtedy kąt β ma miarę
A. 80°
B. 70°
C. 60°
D. 50°

Zadanie nr 40 - maturalne.
Punkt \(A=(3,−5)\) jest wierzchołkiem kwadratu \(ABCD\), a punkt \(M=(1,3)\) jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu \(ABCD\) jest równe
A. \(68\)
B. \(136\)
C. \(2\sqrt{34}\)
D. \(8\sqrt{34}\)

Zadanie nr 41 - maturalne.
Boki równoległoboku mają długości 6 i 10, a kąt rozwarty między tymi bokami ma miarę 120°. Pole tego równoległoboku jest równe
A. \(30\sqrt{3}\)
B. \(30\)
C. \(60\sqrt{3}\)
D. \(60\)

Zadanie nr 42 - maturalne.
Punkty \(A=(−4,4)\) i \(B=(4,0)\) są sąsiednimi wierzchołkami kwadratu ABCD. Przekątna tego kwadratu ma długość
A. \(4\sqrt{10}\)
B. \(4\sqrt{2}\)
C. \(4\sqrt{5}\)
D. \(4\sqrt{7}\)

Zadanie nr 43 - maturalne.
Dany jest prostokąt o bokach długości \(a\) i \(b\), gdzie \(a<b\). Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego.
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F i wpisz te litery w wykropkowanych miejscach.
Zależności między długościami boków tego prostokąta zapisano w układach równań oznaczonych literami: ……… oraz ……… .
A. \(\begin{cases}2ab=30\\a-b=5\end{cases}\)
B. \(\begin{cases}2a+b=30\\a=5b\end{cases}\)
C. \(\begin{cases}2(a+b)=30\\b=a-5\end{cases}\)
D. \(\begin{cases}2a+2b=30\\b=5a\end{cases}\)
E. \(\begin{cases}2a+2b=30\\a-b=5\end{cases}\)
F. \(\begin{cases}a+b=30\\a=b+5\end{cases}\)

Zadanie nr 44 - maturalne.
W rombie o boku długości \(6\sqrt{2}\) kąt rozwarty ma miarę 150°. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Iloczyn długości przekątnych tego rombu jest równy
A. 24
B. 72
C. 36
D. \(36\sqrt{2}\)
Liczba odnalezionych zadań w zbiorze: 44.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.