Zadania — funkcje
Znajdziesz tutaj zadania z takich tematów jak definicja i własności funkcji, w tym dziedzina, monotoniczność funkcji, wykres funkcji, ekstremum, miejsca zerowe funkcji itp. Wszystkie zadania są z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 3.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{3}}{(x-3)}+1\).
Zadanie nr 5.
Naszkicować wykres funkcji \(y=\log_{\frac{1}{2}}{(\sqrt{2}x+2\sqrt{2})}+1\).
Zadanie nr 9.
Sporządzić wykres funkcji
a) \(y+2=\frac{1}{x+3}\)
b) \(y=2+\cos{(x+1)}\)
wykorzystując pomocniczy układ współrzędnych.
Zadanie nr 11.
Dana jest funkcja \(f(x)=\frac{x-3}{x^2+4}+x-1\)
Obliczyć:
a) \(f(1)\)
b) \(f(0)\)
c) \(f(-2)\)
d) \(f(\frac{1}{2})\).
Zadanie nr 12.
Wyznaczyć dziedzinę funkcji
a) \(f(x)=\sqrt{x^2-3x}\)
b) \(f(x)=log_{x-1}{x+1}\)
Zadanie nr 14.
Sporządzić wykres funkcji:
\(f(x)=\begin{cases} -x\ dla\ x<2\\x-1 \ dla\ x\geq 2\end{cases}\).
Zadanie nr 15.
Dane są funkcje:
- \(f(x)=x^2, g(x)=3x+1\)
- \(f(x)=3x+1, g(x)=\log{x}\)
- \(f(x)=2x,\ x> 0, g(x)=\log{x}\)
Znaleźć złożenie funkcji: \((g\circ f)(x)\) i \((f\circ f)(x)\).
Zadanie nr 16.
Dane są funkcje:
- \(f(x)=\cos{x},\ g(x)=\sqrt{x}\)
- \(f(x)=\sin{x},\ g(x)=x^2\)
- \(f(x)=\log{x},\ g(x)=\sqrt{x}\)
Znaleźć złożenie tych funkcji: \((g\circ f)(x)\) i \((f\circ g)(x)\).
Zadanie nr 17.
Wyznaczyć miejsce zerowe funkcji:
a) \(f(x)=3x^2-12x+12\)
b) \(f(x)=-5x+4\)
c) \(f(x)=|x-1|+5\)
Zadanie nr 18.
Wyznaczyć wzór funkcji, której wykresem jest prosta, przechodząca przez punkt \(A= (1,5)\) i która ma jedno miejsce zerowe \(x_0=5\).
Zadanie nr 19.
Wykazać na podstawie definicji, że funkcja \(f(x)=\frac{x}{2}-3\) jest rosnąca w całej swojej dziedzinie.
Zadanie nr 20.
Wykazać na podstawie definicji, że funkcja \(f(x)=5-x\) jest malejąca w całej swojej dziedzinie.
Zadanie nr 21.
Wykazać na podstawie definicji, że funkcja \(f(x)=x^2\) jest rosnąca dla \(x>0\).
Zadanie nr 22.
Sprawdzić, czy funkcja
a) \(f(x)=2x^2-5\)
b) \(f(x)=x^2-5x+4\)
jest parzysta.
Zadanie nr 23.
Sprawdzić, czy funkcja
a) \(f(x)=\frac{x-5}{4}\)
b) \(f(x)=-5x^3\)
jest nieparzysta.
Zadanie nr 24.
Znaleźć okres podstawowy funkcji
a) \(y=\sin{2x}\)
b) \(y= \sin{\pi x}\)
Zadanie nr 27.
Znaleźć okres podstawowy funkcji: \(y=\frac{1}{2}tg{(\frac{\pi}{2}x)}\).
Zadanie nr 28.
Znaleźć okres podstawowy funkcji:
a) \(y=3ctg{\frac{x}{\pi}}\)
b) \(y=2\cos{(x+\frac{\pi}{7})}\)
Zadanie nr 30.
Znaleźć okres podstawowy funkcji: \(y=\cos^4{x}-\sin^4{x}\).

Zadanie nr 31 - maturalne.
Dana jest funkcja liniowa \(f(x)=\frac{3}{4}x+6\). Miejscem zerowym tej funkcji jest liczba:
A. \(8\)
B. \(6\)
C. \(-6\)
D. \(-8\)

Zadanie nr 32 - maturalne.
Funkcja f określona jest wzorem \(f(x)=\frac{2x^3}{x^6+1}\) dla każdej liczby rzeczywistej \(x\). Wtedy \(f(-\sqrt[3]{3})\) jest równa:
A. \(-\frac{\sqrt[3]{9}}{2}\)
B. \(-\frac{3}{5}\)
C. \(\frac{3}{5}\)
D. \(\frac{3}{5}\)

Zadanie nr 33 - maturalne.
Na rysunku przedstawiono wykres funkcji \(f\).
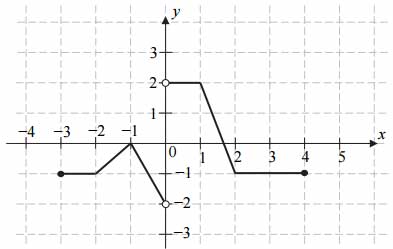
Zbiorem wartości funkcji \(f\) jest
A. \((-2,2)\)
B. \([-2,2)\)
C. \([-2,2]\)
D. \((-2,2]\)

Zadanie nr 34 - maturalne.
Funkcja kwadratowa określona jest wzorem \(f(x)=x^2+x+c\). Jeżeli \(f(3)=4\), to:
A. \(f(1)=-6\)
B. \(f(1)=0\)
C. \(f(1)=6\)
D. \(f(1)=18\)

Zadanie nr 35 - maturalne.
Do wykresu funkcji, określonej dla wszystkich liczb rzeczywistych wzorem \(y=-2^{x-2}\), należy punkt:
A. \(A=(1,-2)\)
B. \(B=(2,-1)\)
C. \(C=(1,\frac{1}{2})\)
D. \(D=(4,4)\)

Zadanie nr 36 - maturalne.
Na rysunku przedstawiono fragment wykresu funkcji \(f\), który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem \(y=\frac{1}{x}\) dla każdej liczby rzeczywistej \(x\neq 0\).
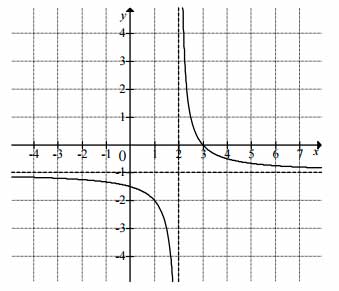
a) Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji \(f\) są większe od \(0\).
b) Podaj miejsce zerowe funkcji \(g\) określonej wzorem \(g(x)=f(x-3)\).

Zadanie nr 37 - maturalne.
Miejscem zerowym funkcji liniowej \(f(x)=\sqrt{3}(x+1)-12\) jest liczba
A. \(\sqrt{3}-4\)
B. \(-2\sqrt{3}+1\)
C. \(4\sqrt{3}-1\)
D. \(-\sqrt{3}+12\)

Zadanie nr 38 - maturalne.
Miejscem zerowym funkcji liniowej \(f\) określonej wzorem \(f(x)=3(x+1)−6\sdqrt{3}\) jest liczba
A. \(3−6\sqrt{3}\)
B. \(1−6\sqrt{3}\)
C. \(2\sqrt{3}-1\)
D. \(2\sqrt{3}-\frac{1}{3}\)

Zadanie nr 39 - maturalne.
Punkt \(A=(\frac{1}{3},-1)\) należy do wykresu funkcji liniowej \(f\) określonej wzorem \(f(x)=3x+b\). Wynika stąd, że
A. \(b=2\)
B. \(b=1\)
C. \(b=-1\)
D. \(b=-2\)

Zadanie nr 40 - maturalne.
Na poniższym rysunku przedstawiono wykres funkcji \(f\) określonej w zbiorze \([−6, 5]\).
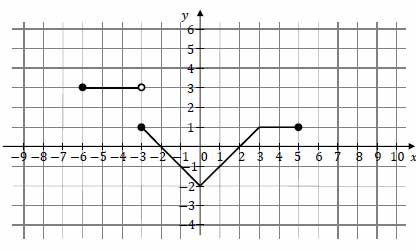
Funkcja \(g\) jest określona wzorem \(g(x)=f(x)-2\) dla \(x\in [−6, 5]\). Wskaż zdanie prawdziwe.
A. Liczba \(f(2)+g(2)\) jest równa \((−2)\).
B. Zbiory wartości funkcji \(f\) i \(g\) są równe.
C. Funkcje \(f\) i \(g\) mają te same miejsca zerowe.
D. Punkt \(P=(0,−2)\) należy do wykresów funkcji \(f\) i \(g\).

Zadanie nr 41 - maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^2}{(2x-2)}\) dla każdej liczby rzeczywistej \(x \neq 1\). Wtedy dla argumentu \(x=\sqrt{3}-1\) wartość funkcji \(f\) jest równa
A. \(\frac{1}{\sqrt{3}-1)}\)
B. \(-1\)
C. \(1\)
D. \(\frac{1}{(\sqrt{3}-2)}\)

Zadanie nr 42 - maturalne.
Do wykresu funkcji \(f\) określonej dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=3^x-2\) należy punkt o współrzędnych
A. \((-1,-5)\)
B. \((0,-2)\)
C. \((0,-1)\)
D. \((2,4)\)

Zadanie nr 43 - maturalne.
Funkcja liniowa \(f\) przyjmuje wartość \(2\) dla argumentu \(0\), a ponadto \(f(4)-f(2)=6\). Wyznacz wzór funkcji \(f\).

Zadanie nr 44 - maturalne.
Na rysunku przedstawiono wykres funkcji \(f\).
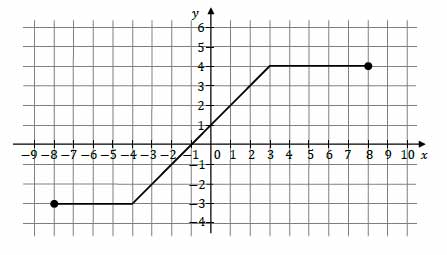
Iloczyn \(f(-3)\cdot f(0)\cdot f(4)\) jest równy
A. (-12)
B. (-8)
C. 0
D. 16

Zadanie nr 45 - maturalne.
Na rysunku 1. przedstawiono wykres funkcji \(f\) określonej na zbiorze \(\langle -4; 5\rangle\).
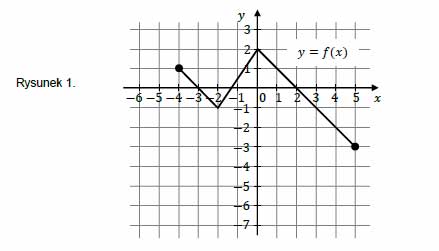
Funkcję \(g\) określono za pomocą funkcji \(f\). Wykres funkcji \(g\) przedstawiono na rysunku 2.
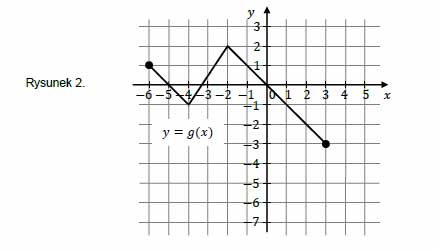
Wynika stąd, że
A. \(g(x)=f(x)-2\)
B. \(g(x)=f(x-2)\)
C. \(g(x)=f(x)+2\)
D. \(g(x)=f(x+2)\)

Zadanie nr 46 - maturalne.
Miejscem zerowym funkcji liniowej \(f\) określonej wzorem \(f(x)=\frac{1}{3}(x+3)+5\) jest liczba
A. (-3)
B. \(\frac{9}{2}\)
C. 5
D. 12

Zadanie nr 47 - maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) narysowano wykres funkcji \(y=f(x)\) (zobacz rysunek).
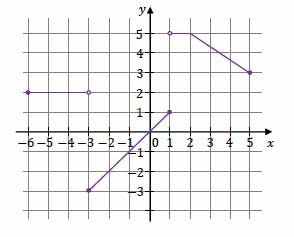
1. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Dziedziną funkcji \(f\) jest zbiór
A. \([−6,5]\)
B. \((−6,5)\)
C. \((−3,5]\)
D. \([−3,5]\)
2. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Największa wartość funkcji \(f\) w przedziale \([−4,1]\) jest równa
A. \(0\)
B. \(1\)
C. \(2\)
D. \(5\)
3. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Funkcja \(f\) jest malejąca w zbiorze
A. \([−6,−3)\)
B. \([−3,1]\)
C. \((1,2]\)
D. \([2,5]\)

Zadanie nr 48 - maturalne.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę \(L\) obsługiwanych klientów \(n\)-tego dnia opisuje funkcja \(L(n)=-n^2+22n+279\), gdzie \(n\) jest liczbą naturalną spełniającą warunki \(n\geq 1\) i \(n\leq 30\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz \(P\), jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
| Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa \(L(30)\). | P | F |
| W trzecim dniu analizowanego okresu obsłużono 336 klientów. | P | F |
Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia. Zapisz obliczenia.
Liczba odnalezionych zadań w zbiorze: 48.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.




