Zadania — przekształcenia geometryczne
Znajdziesz tutaj zadania z przekształceń geometrycznych. To zadania z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 1.
Znaleźć równanie symetralnej odcinka \(\overline{AB}\), gdzie \(A=(1,4), \ B=(-2, 1)\).
Zadanie nr 2.
Dany jest trójkąt równoboczny o boku a. Środki boków tego trójkąta dzielą dany trójkąt na mniejsze części. Wykaż, że wszystkie mniejsze trójkąty są przystające i są trójkątami równobocznymi.
Zadanie nr 3.
Znaleźć równanie dwusiecznej kątów wyznaczonych przez proste o równaniach \(y=-\frac{3}{4}x+\frac{1}{2}\) i \(y=\frac{4}{3}x+\frac{5}{3}\).
Zadanie nr 4.
Znaleźć obraz okręgu i trapezu na prostą \(a\) w kierunku prostej \(k\).
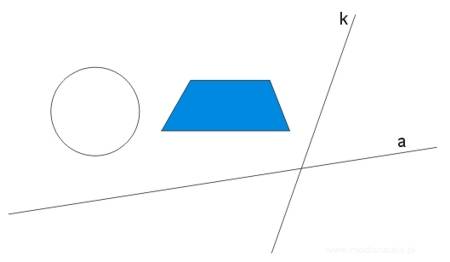
Zadanie nr 5.
Obrazem kwadratu w rzucie równoległym na prostą \(a\) jest jego przekątna. Znaleźć kierunek rzutowania.
Zadanie nr 6.
Znaleźć obraz punktu \(P=(0,2)\) w rzucie równoległym na oś \(OX\) w kierunku prostej \(y=2x-3\).
Zadanie nr 7.
Znaleźć obraz punktu \(P=(2,3)\) w rzucie prostokątnym na prostą \(y=-x+2\).
Zadanie nr 8.
Znaleźć obraz okręgu \((x-2)^2+(y-1)^2=4\) w rzucie prostokątnym na prostą \(y=x\).
Zadanie nr 9.
Znaleźć obraz kwadratu w rzucie prostokątnym na prostą przechodzącą przez środki dwóch sąsiadujących boków.
Zadanie nr 10.
Znaleźć obraz kwadratu w symetrii osiowej względem prostej przechodzącej przez środki dwóch sąsiadujących boków tego kwadratu.
Zadanie nr 11.
Znaleźć obraz trójkąta prostokątnego w symetrii osiowej względem prostej przechodzącej przez tylko jeden z wierzchołków trójkąta równoległej do przyprostokątnej tego trójkąta.
Zadanie nr 12.
Znaleźć obraz trójkąta \(ABC\), gdzie \(A=(-2,3), B=(2,4), C=(2,-2)\) w symetrii osiowej względem osi \(OX\) i \(OY\).
Zadanie nr 13.
Znaleźć obraz krzywej \(y=3x^2-2x+1\) w symetrii osiowej względem osi \(OX\) i \(OY\).
Zadanie nr 14.
Znaleźć obraz okręgu \((x+2)^2+(y-1)^2=4\) w symetrii osiowej względem osi \(OY\). Sporządź odpowiednie wykresy w układzie współrzędnych.
Zadanie nr 15.
Znaleźć oś symetrii trójkąta \(ABC\), gdzie \(A=(1,1), B=(5,1), C=(3,3)\).
Zadanie nr 16.
Znaleźć obraz trójkąta równobocznego w symetrii środkowej względem dowolnego wierzchołka tego trójkąta.
Zadanie nr 17.
Znaleźć obraz kwadratu w przekształceniu będącym złożeniem czterech symetrii środkowych względem kolejnych wierzchołków tego kwadratu.
Zadanie nr 18.
Znaleźć obraz trójkąta \(BC\) w symetrii środkowej względem początku układu współrzędnych, jeżeli \(A=(-2,3), B=(5,3), C=(0,7)\).
Zadanie nr 19.
Znaleźć obraz krzywej \(y=x^3-x^2\) w symetrii środkowej względem początku układu współrzędnych.
Zadanie nr 20.
Znaleźć obraz kwadratu \(ABCD\), gdzie \(A=(1,1), B=(2,3), C=(4,2), D=(3,0)\) w translacji o wektor \(\vec{w}=[-2,-1]\).
Zadanie nr 21.
Znaleźć obraz krzywej \(y=-x^2+x-1\) w translacji o wektor \(\vec{w}=[-2,1]\).
Zadanie nr 22.
Obrazem punktu \(P=(7,-3)\) w translacji o wektor \(\vec{w}\) jest punkt \(P'=(-3,7)\). Znaleźć współrzędne wektora translacji.
Zadanie nr 23.
Znaleźć obraz punktu \(P=(2,4)\) w obrocie dookoła początku układu współrzędnych o kąt \(30°\).
Zadanie nr 24.
Znaleźć obraz krzywej \(y=x^3\) w obrocie dookoła początku układu współrzędnych o kąt \(90°\).
Zadanie nr 25.
Znaleźć obraz prostej \(y=-2x+6\) w obrocie dookoła początku układu współrzędnych o kąt \(60°\).
Zadanie nr 26.
Znaleźć obraz kwadratu w jednokładności o środku w jednym z wierzchołków tego kwadratu i skali \(k=2\).
Zadanie nr 27.
Znaleźć obraz trójkąta prostokątnego w jednokładności o środku w punkcie, który jest środkiem przeciwprostokątnej tego trójkąta i skali \(k=-\frac{1}{2}\).
Zadanie nr 28.
Znaleźć obraz odcinka \(\overline{AB}\), gdzie \(A=(-1,2), B=(-2,-3)\) w jednokładności o środku w początku układu współrzędnych i skali \(k=3\). Zilustrować to przekształcenie w układzie współrzędnych.
Zadanie nr 29.
Znaleźć obraz krzywej \(y=x^2\) w jednokładności o środku w początku układu współrzędnych i skali \(k=\frac{1}{2}\). Zilustrować to przekształcenie w układzie współrzędnych.
Zadanie nr 30.
Znaleźć obraz wykresu funkcji \(y=|x|\) w obrocie dookoła początku układu współrzędnych o kąt \(45°\).
Zadanie nr 31 - maturalne.
Przedstawione na rysunku trójkąty \(ABC\) i \(PQR\) są podobne. Bok \(AB\) trójkąta \(ABC\) ma długość
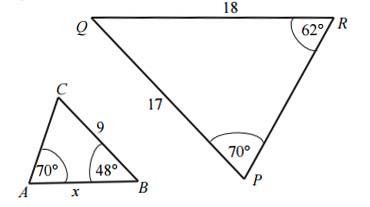
A. 8
B. 8,5
C. 9,5
D. 10
Zadanie nr 32 - maturalne.
Dany jest trójkąt prostokątny \(ABC\). Na przyprostokątnych \(AC\) i \(AB\) tego trójkąta obrano odpowiednio punkty \(D\) i \(G\). Na przeciwprostokątnej \(BC\) wyznaczono punkty \(E\) i \(F\) takie, że \(|\angle DEC|=|\angle BGF|=90°\) (zobacz rysunek). Wykaż, że trójkąt \(CDE\) jest podobny do trójkąta \(FBG\).
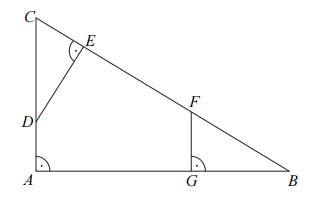
Zadanie nr 33 - maturalne.
Dany jest prostokąt \(ABCD\). Okrąg wpisany w trójkąt \(BCD\) jest styczny do przekątnej \(BD\) w punkcie \(N\). Okrąg wpisany w trójkąt \(ABD\) jest styczny do boku \(AD\) w punkcie \(M\), a środek \(S\) tego okręgu leży na odcinku \(MN\), jak na rysunku.
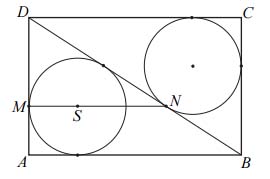
Wykaż, że \(|MN|=|AD|\).
Zadanie nr 34 - maturalne.
Dane są punkty \(M = (-2,1), N = (-1,3)\). Punkt \(K \)jest środkiem odcinka \(MN\). Obrazem punktu \(K\) w symetrii względem początku układu współrzędnych jest punkt:
A. \(K'=(2,-\frac{3}{2})\)
B. \(K'=(2,\frac{3}{2})\)
C. \(K'=(\frac{3}{2},2)\)
D. \(K'=(\frac{3}{2},-2)\)
Zadanie nr 35 - maturalne.
Dwusieczne czworokąta \(ABCD\) wpisanego w okrąg przecinają się w czterech różnych punktach: \(P, Q, R, S\) (zobacz rysunek).
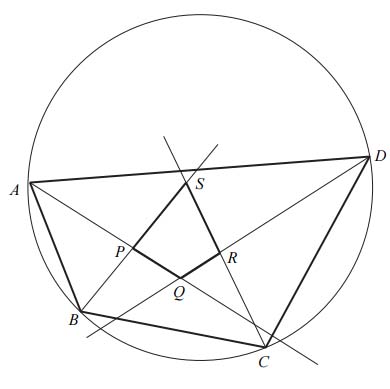
Wykaż, że na czworokącie \(PQRS\) można opisać okrąg.
Zadanie nr 36 - maturalne.
Jeżeli trójkąty \(ABC\) i \(A'B'C'\) są podobne, a ich pola są, odpowiednio, równe 25 cm2 i 50 cm2, to skala podobieństwa \(\frac{A'B'}{AB}\) jest równa:
A. \(2\)
B. \(\frac{1}{2}\)
C. \(\sqrt{2}\)
D. \(\frac{\sqrt{2}}{2}\)
Zadanie nr 37 - maturalne.
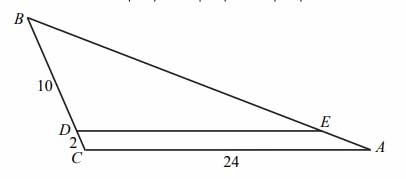
W trójkącie \(ABC\) punkt \(D\) leży na boku \(BC\), a punkt \(E\) leży na boku \(AB\). Odcinek \(DE\) jest równoległy do boku \(AC\), a ponadto \(|BD|=10, |BC|=12\) i \(|AC|=24\) (zobacz rysunek).
A. \(m=22\)
B. \(m=20\)
C. \(m=12\)
D. \(m=11\)
Długość odcinka DE jest równa
Zadanie nr 38 - maturalne.
Dany jest trójkąt o bokach długości: \(2\sqrt{5}, 3\sqrt{5}. 4\sqrt{5}\). Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości:
A. \(10, 15, 20\)
B. \(20, 45, 80\)
C. \(\sqrt{2}, \sqrt{3}, \sqrt{4}\)
D. \(\sqrt{5}, 2\sqrt{5}, 3\sqrt{5}\)
Zadanie nr 39 - maturalne.
Trójkąt \(ABC\) jest ostrokątny oraz \(|AC|>|BC|\). Dwusieczna \(d_C\) kąta \(ACB\) przecina bok \(AB\) w punkcie \(K\). Punkt \(L\) jest obrazem punktu \(K\) w symetrii osiowej względem dwusiecznej \(d_A\) kąta \(BAC\), punkt \(M\) jest obrazem punktu \(L\) w symetrii osiowej względem dwusiecznej \(d_C\) kąta \(ACB\), a punkt \(N\) jest obrazem punktu \(M\) w symetrii osiowej względem dwusiecznej \(d_B\) kąta \(ABC\) (zobacz rysunek).
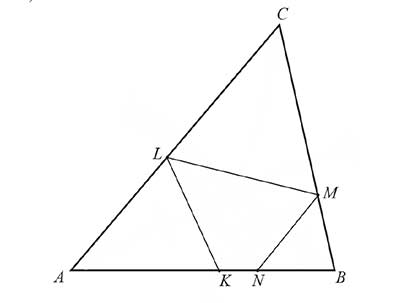
Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.
Zadanie nr 40 - maturalne.
Dane są dwa okręgi: okrąg o środku w punkcie \(O\) i promieniu \(5\) oraz okrąg o środku w punkcie \(P\) i promieniu \(3\). Odcinek \(OP\) ma długość \(16\). Prosta \(AB\) jest styczna do tych okręgów w punktach \(A\) i \(B\). Ponadto prosta \(AB\) przecina odcinek \(OP\) w punkcie \(K\) (zobacz rysunek).
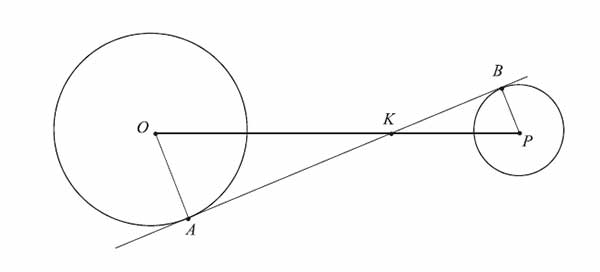
Wtedy
A. \(|OK|=6\)
B. \(|OK|=8\)
C. \(|OK|=10\)
D. \(|OK|=12\)
Zadanie nr 41 - maturalne.
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej f. Na wykresie tej funkcji leżą punkty \(A=(0,4)\) i \(B=(2,2)\).
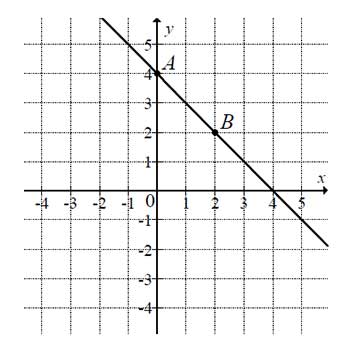
Obrazem prostej \(AB\) w symetrii względem początku układu współrzędnych jest wykres funkcji \(g\) określonej wzorem
A. \(g(x)=x+4\)
B. \(g(x)=x-4\)
C. \(g(x)=-x-4\)
D. \(g(x)=-x+4\)
Zadanie nr 42 - maturalne.
Punkt B jest obrazem punktu \(A=(−3,5)\) w symetrii względem początku układu współrzędnych. Długość odcinka \(AB\) jest równa
A. \(2\sqrt{34}\)
B. \(8\)
C. \(\sqrt{34}\)
D. \(12\)
Zadanie nr 43 - maturalne.
Trójkąt \(ABC\) jest równoboczny. Punkt \(E\) leży na wysokości \(CD\) tego trójkąta oraz \(|CE|=\frac{3}{4}|CD|\). Punkt \(F\) leży na boku \(BC\) i odcinek \(EF\) jest prostopadły do \(BC\) (zobacz rysunek).
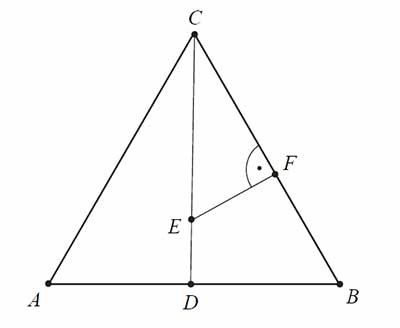
Wykaż, że \(|CF|=\frac{9}{16}|CB|\).
Zadanie nr 44 - maturalne.
Prosta o równaniu \(x+y−10=0\) przecina okrąg o równaniu \(x^2+y^2−8x−6y+8=0\) w punktach \(K\) i \(L\). Punkt \(S\) jest środkiem cięciwy \(KL\). Wyznacz równanie obrazu tego okręgu w jednokładności o środku \(S\) i skali \(k=−3\).
Zadanie nr 45 - maturalne.
Trójkąt równoboczny \(ABC\) ma pole równe \(9\sqrt{3}\). Prosta równoległa do boku \(BC\) przecina boki \(AB\) i \(AC\) — odpowiednio — w punktach \(K\) i \(L\). Trójkąty \(ABC\) i \(AKL\) są podobne, a stosunek długości boków tych trójkątów jest równy \(\frac{3}{2}\). Oblicz długość boku trójkąta \(AKL\).
Zadanie nr 46 - maturalne.
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Dwusieczna kąta \(BAC\) przecina bok \(BC\) w takim punkcie \(D\), że trójkąty \(ABC\) i \(BDA\) są podobne (zobacz rysunek). Oblicz miarę kąta \(BAC\).
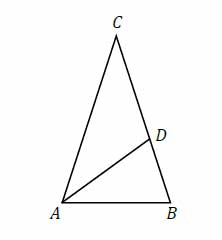
Zadanie nr 47 - maturalne.
Trójkąty prostokątne \(T_1\) i \(T_2\) są podobne. Przyprostokątne trójkąta \(T_1\) mają długości 5 i 12. Przeciwprostokątna trójkąta \(T_2\) ma długość 26. Oblicz pole trójkąta \(T_2\). Zapisz obliczenia.
Liczba odnalezionych zadań w zbiorze: 47.
Oznaczenia
Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom rozszerzony.
