Zadania z matematyki
Znajdziesz tutaj rozwiązania zadań z matematyki prezentowanych w lekcjach i artykułach. Zadanie zwykle ma dwa rodzaje rozwiązań: uproszczone, które zawiera jedynie niektóre kroki rozwiązania zadania oraz ze szczegółowymi wyjaśnieniami, rysunkami, ze wszystkimi pomocniczymi rachunkami.
Liczba wszystkich zadań w niniejszym zbiorze: 1149
Wyszukaj zadanie
Wpisz w poniższe pola formularza fragment treści zadania lub wzoru (używając składni LaTeX-a). Wyszukiwarka wyświetli pierwszych 20 wyników wyszukiwania i linki do nastepnych stron.
Zadanie nr 1 — maturalne.
W kartezjańskim układzie współrzędnych \((x,y)\) prosta \(l\) o równaniu \(x-y-2=0\) przecina parabolę o równaniu \(y=4x^2-7x+1\) w punktach \(A\) oraz \(B\). Odcinek \(AB\) jest średnicą okręgu \(O\). Punkt \(C\) leży na okręgu \(O\) nad prostą \(l\), a kąt \(BAC\) jest ostry i ma miarę \(\alpha\) taką, że \(tg\alpha=\frac{1}{3}\) (zobacz rysunek).
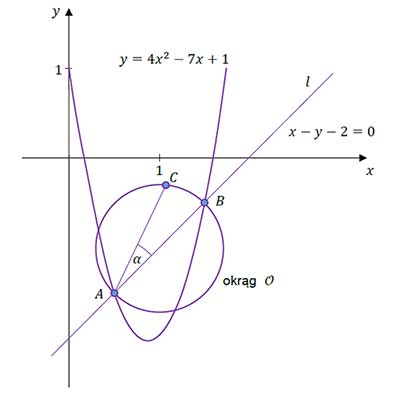
Oblicz współrzędne punktu \(C\). Zapisz obliczenia.
Zadanie nr 2 — maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=81^{\log_3{x}}+\frac{2\cdot\log_2 {\sqrt{7}}\cdot \log_3{2}}{3}\cdot x^2-6x\) dla każdej liczby dodatniej \(x\).
1. Wykaż, że dla każdej liczby dodatniej \(x\) wyrażenie \(81^{\log_3{x}}+\frac{2\cdot\log_2 {\sqrt{7}}\cdot \log_3{2}}{3}\cdot x^2-6x\) można równoważnie przekształcić do postaci \(x^4+x^2-6x\).
2. Oblicz najmniejszą wartość funkcji \(f\) określonej dla każdej liczby dodatniej \(x\). Zapisz obliczenia. Wskazówka: przyjmij, że wzór funkcji \(f\) można przedstawić w postaci \(f(x)=x^4+x^2-6x\).
Zadanie nr 3 — maturalne.
Wyznacz wszystkie wartości parametru \(m\neq 2\), dla których równanie
\(x^2+4x-\frac{m-3}{m-2}=0\)
ma dwa różne rozwiązania rzeczywiste \(x_1, x_2\) spełniające warunek \(x_1^3+x_2^3>-28\). Zapisz obliczenia.
Zadanie nr 4 — maturalne.
Określamy kwadraty \(K_1, K_2, K_3, ...\) następująco:
• \(K_1\) jest kwadratem o boku długości \(a\).
• \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1:3\).
• \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1:3\).
i ogólnie, dla każdej liczby naturalnej \(n\geq 2\)
• \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_n-1\) i dzieli ten bok w stosunku \(1:3\).
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
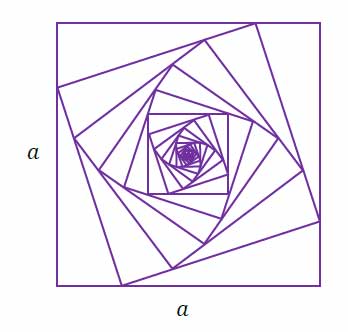
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu. Zapisz obliczenia.
Zadanie nr 5 — maturalne.
Rozwiąż nierówność:
\(\sqrt{x^2+4x+4}<\frac{25}{3}-\sqrt{x^2-6x+9}\)
Zapisz obliczenia. Wskazówka: skorzystaj z tego, że \(\sqrt{a^2}=|a|\) dla każdej liczby rzeczywistej \(a\).
Zadanie nr 6 — maturalne.
Czworokąt \(ABCD\), w którym \(|BC|=4\) i \(|CD=5|\), jest opisany na okręgu. Przekątna \(AC\) tego czworokąta tworzy z bokiem \(BC\) kąt o mierze 60°, natomiast z bokiem \(AB\) – kąt ostry, którego sinus jest równy \(\frac{1}{4}\) . Oblicz obwód czworokąta \(ABCD\). Zapisz obliczenia.
Zadanie nr 7 — maturalne.
Dany jest sześcian \(ABCDEFGH\) o krawędzi długości 6. Punkt \(S\) jest punktem przecięcia przekątnych \(AH\) i \(DE\) ściany bocznej \(ADHE\) (zobacz rysunek).
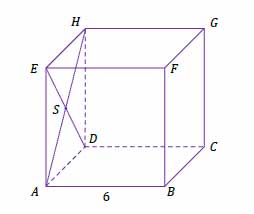
Oblicz wysokość trójkąta \(SBH\) poprowadzoną z punktu \(S\) na bok \(BH\) tego trójkąta. Zapisz obliczenia.
Zadanie nr 8 — maturalne.
Rozwiąż równanie \(4\sin{(4x)}\cos{(6x)}=2\sin{(10x)}+1\). Zapisz obliczenia.
Zadanie nr 9 — maturalne.
Dany jest trójkąt prostokątny \(ABC\), w którym \(|\angle ABC|=90°\) oraz \(|\angle CAB|=60°\). Punkty \(K\) i \(L\) leżą na bokach – odpowiednio – \(AB\) i \(BC\) tak, że \(|BK|=|BL|=1\) (zobacz rysunek). Odcinek \(KL\) przecina wysokość \(BD\) tego trójkąta w punkcie \(N\), a ponadto \(|AD|=2\).
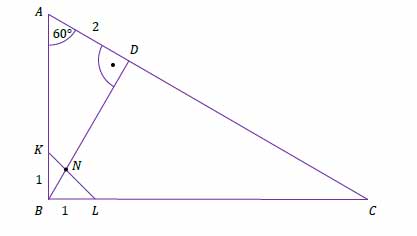
Wykaż, że \(|ND|=\sqrt{3}+1\).
Zadanie nr 10 — maturalne.
Liczby rzeczywiste \(x\) oraz \(y\) spełniają jednocześnie równanie \(x+y=4\) i nierówność \(x^3-x^2y\leq xy^2-y^3\). Wykaż, że \(x=2\) oraz \(y=2\).
Zadanie nr 11 — maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{3x^2-2x}{x^2+2x+8}\) dla każdej liczby rzeczywistej \(x\). Punkt \(P=(x_0,3)\) należy do wykresu funkcji \(f\). Oblicz \(x_0\) oraz wyznacz równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\). Zapisz obliczenia.
Zadanie nr 12 — maturalne.
Tomek i Romek postanowili rozegrać między sobą pięć partii szachów. Prawdopodobieństwo wygrania pojedynczej partii przez Tomka jest równe \(\frac{1}{4}\). Oblicz prawdopodobieństwo wygrania przez Tomka co najmniej czterech z pięciu partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego. Zapisz obliczenia.
Zadanie nr 13 — maturalne.
W chwili początkowej (\(t=0\)) masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 19% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej \(t\geq 0\) funkcja \(m(t)\) określa masę substancji w gramach po \(t\) pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji \(m(t)\). Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od \(1,5\) grama. Zapisz obliczenia.
Zadanie nr 14 — maturalne.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę \(L\) obsługiwanych klientów \(n\)-tego dnia opisuje funkcja \(L(n)=-n^2+22n+279\), gdzie \(n\) jest liczbą naturalną spełniającą warunki \(n\geq 1\) i \(n\leq 30\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz \(P\), jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
| Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa \(L(30)\). | P | F |
| W trzecim dniu analizowanego okresu obsłużono 336 klientów. | P | F |
Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia. Zapisz obliczenia.
Zadanie nr 15 — maturalne.
Ze zbioru ośmiu liczb {2,3,4,5,6,7,8,9} losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez \(15\). Zapisz obliczenia.
Zadanie nr 16 — maturalne.
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.
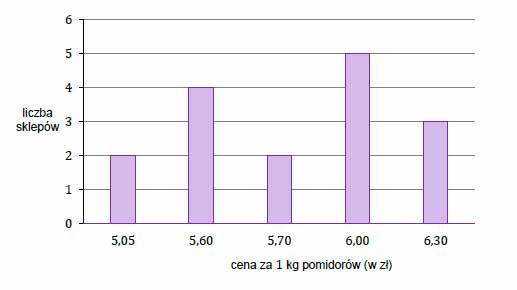
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.
| 1. | Mediana ceny kilograma pomidorów w tych wybranych sklepach jest równa | |
| 2. | Średnia cena kilograma pomidorów w tych wybranych sklepach jest równa |
A. 5,80 zł
B. 5,73 zł
C. 5,85 zł
D. 6 zł
E. 5,70 zł
Zadanie nr 17 — maturalne.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0, 5, 7 (np. 57 075, 55 555), jest
A. \(5^3\)
B. \(2\cdot 4^3\)
C. \(2\cdot 3^4\)
D. \(3^5\)
Zadanie nr 18 — maturalne.
W pewnym ostrosłupie prawidłowym stosunek liczby \(W\) wszystkich wierzchołków do liczby \(K\) wszystkich krawędzi jest równy \(\frac{W}{K}=\frac{3}{5}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Podstawą tego ostrosłupa jest
A. kwadrat.
B. pięciokąt foremny.
C. sześciokąt foremny.
D. siedmiokąt foremny.
Zadanie nr 19 — maturalne.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30° i ma długość równą 6 (zobacz rysunek).
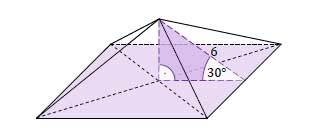
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.
Zadanie nr 20 — maturalne.
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem \(\alpha\) takim, że \(\cos{\alpha}=\frac{\sqrt{2}}{3}\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Długość przekątnej tego graniastosłupa jest równa
A. \(15\sqrt{2}\)
B. \(45\)
C. \(5\sqrt{2}\)
D. \(10\)
Jak znaleźć w inny sposób zadanie w serwisie?
Jest kilka innych sposobów na odszukanie danego zadania w zbiorze zadań w niniejszym serwisie.
- Przejdź do działu Matematyka i wybierz ze spisu treści odpowiedni artykuł. Do większości z nich dołączono zbiór zadań powiązanych tematycznie. W ten sposób znajdziesz zadania, gdy wiesz z jakim tematem są związane.
- Przejdź do wyszukiwarki i wpisz w pole formularza fragment treści zadania. Skorzystaj z tej opcji, jeżeli nie potrafisz określić działu matematyki.
Rozwiązywanie zadań jest najlepszym sposobem na weryfikację posiadanej wiedzy. Umiejętność rozwiązywania zadań wymaga wielu ćwiczeń, do których zachęcam. Wszystkie zadania zostały przyporządkowane do właściwych rozdziałów z danego przedmiotu oraz lekcji i artykułów. Zadania są na różnym poziomie trudności. Nauka materiału pozwoli przygotować się świetnie do lekcji oraz do egzaminu maturalnego lub gimnazjalnego.
Jak tworzyć zapytania dla wyszukiwarki zadań?
Poniżej znajdziesz podstawowe informacje na temat wyszukiwania zadań w oparciu o składnię LaTeX-a wraz z przykładami. Zawarto tu jedynie opis najbardziej podstawowych wyrażeń. W zadaniach stosowane są także inne formuły, których tu nie będziemy omawiać. Zainteresowanych odsyłamy do opisu języka znaczników LaTeX.
Dla większej celności wyników wyszukiwania w swoich zapytaniach staraj się unikać znaku "\".
![]() Ułamki
Ułamki
Ułamek a/b zapisujemy w LaTeX za pomocą wyrażenia \frac{a}{b}.
Przykład: Aby wyszukać w zbiorze wszystkie zadania, w treści których występuje ułamek 1/4 wpisz w pole wyszukiwania wyrażenie frac{1}{4}.
![]() Potęga i indeks górny
Potęga i indeks górny
Potęgę/indeks górny ab zapisujemy w LaTeX za pomocą wyrażenia a^b.
Przykład: Aby wyszukać w zbiorze wszystkie zadania, w treści których występuje wyrażenie x2+2x wpisz w pole wyszukiwania wyrażenie x^2+2x.
![]() Pierwiastek
Pierwiastek
Pierwiastek n-tego stopnia z liczby a zapisujemy w LaTeX za pomocą wyrażenia \sqrt[n]{a}.
Przykład: Aby wyszukać w zbiorze wszystkie zadania, w treści których występuje pierwiastek wadratowy z 3 wpisz w pole wyszukiwania wyrażenie sqrt{3}.
![]() Wektor
Wektor
Wektor ![]() w LaTeX opisujemy za pomocą wyrażenia \vec{c}.
w LaTeX opisujemy za pomocą wyrażenia \vec{c}.
Przykład: Aby wyszukać w zbiorze wszystkie zadania, w treści których występuje wektor ![]() wpisz w pole wyszukiwania wyrażenie vec{c}.
wpisz w pole wyszukiwania wyrażenie vec{c}.
![]() Zanki specjalne
Zanki specjalne
znak ≥ - geq
znak ≤ - leq
