Zadania — ciągi liczbowe
Znajdziesz tutaj zadania z ciągów liczbowych arytmetycznych i geometrycznych. To zadania z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 3.
Zamienić liczbę 0,(c) na ułamek zwykły, gdzie \(c\in \lbrace 1,2,3,4,5,6,7,8,9\rbrace\).
Zadanie nr 4.
Środki kwadratu o boku długości a połączono ze sobą. W ten sposób został utworzony kwadrat, którego środki boków znów połączono ze sobą i tak dalej. Obliczyć pole powierzchni wszystkich utworzonych w ten sposób figur geometrycznych.
Zadanie nr 5.
Nieskończenie wiele odcinków, każdy o długości stanowiącej 1/3 długości poprzedniego, ustawiono w linii prostej jeden za drugim. Jakiej długości linijki trzeba dysponować, aby zmierzyć ich łączną długość, jeżeli najdłuższy odcinek ma długość 5 cm?
Zadanie nr 7.
Obliczyć \(1-\frac{1}{\sqrt{2}}+\frac{1}{2}-\frac{1}{2\sqrt{2}}+...\).
Zadanie nr 8.
Rozwiązać równanie \(5+\frac{5}{x}+\frac{5}{x^2}+\frac{5}{x^3}+...=10\).
Zadanie nr 10.
Dla jakich wartości parametru \(x\) szereg geometryczny \(1+x^3+x+1+(x^3+x+1)^2+(x^3+x+1)^3+...\) jest zbieżny?
Zadanie nr 11.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{-n^2-4n+1}{n^2+2}-5)\).
Zadanie nr 12.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}(\frac{n^3+n^2+2n+3}{n+1}-n^2)\).
Zadanie nr 13.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\sqrt{n}=+\infty\).
Zadanie nr 14.
Wykazać na podstawie definicji granicy niewłaściwej, że \(\displaystyle\lim_{n\to\infty}(1+2n)=+\infty\).
Zadanie nr 15.
Wykazać, że \(\displaystyle\lim_{n\to\infty}\frac{1-n^2}{n}=-\infty\).
Zadanie nr 17.
Wykazać na podstawie definicji, że \(\displaystyle\lim_{n\to\infty}\frac{2n+3}{n}=2\).
Zadanie nr 18.
Obliczyć granicę \(\displaystyle\lim_{n\to\infty}\frac{1+2+3+...+n}{n^2+n-1}\).
Zadanie nr 19.
Znaleźć wzór na n-ty wyraz ciągu geometrycznego: \((2+\sqrt{2},2+2\sqrt{2},4+2\sqrt{2},4+4\sqrt{2},...)\).
Zadanie nr 20.
Piąty wyraz ciągu geometrycznego jest równy \(\frac{1}{\sqrt{2}}\), a siódmy \(\sqrt{2}\). Znaleźć dziewiąty wyraz ciągu i obliczyć sumę pierwszych dziesięciu wyrazów tego ciągu geometrycznego.
Zadanie nr 21.
Pierwszy wyraz ciągu geometrycznego jest równy 8, iloraz tego ciągu jest równy 1/2. Obliczyć sumę wyrazów tego ciągu od wyrazu czwartego do dziesiątego.
Zadanie nr 22.
Dla jakich wartości \(x\) i \(y\) ciąg \((5,x,y,\frac{1}{25})\) jest ciągiem geometrycznym?
Zadanie nr 23.
Głębokość basenu w kształcie prostopadłościanu, który mieści milion litrów wody, wynosi 2,5 m. Głębokość, szerokość i długość basenu tworzą ciąg geometryczny. Jaka jest długość i szerokość basenu?
Zadanie nr 24.
Ile metrów studni można wykopać za 1000 zł, jeśli wykonawca oferuje wykopanie pierwszego metra za 1 grosz, a za każdy następny metr dwa razy więcej niż za poprzedni?
Zadanie nr 25.
Znaleźć wzór na n-ty wyraz ciągu:
\((\frac{1}{2}+\frac{\sqrt{2}}{2}, 1+\sqrt{2}, \frac{3}{2}+\frac{3\sqrt{2}}{2},2+2\sqrt{2}, ...)\)
Zadanie nr 26.
Wykazać, że ciąg \(a_n=\frac{n\sqrt{2}+n}{3}\) jest ciągiem arytmetycznym.
Zadanie nr 28.
Znaleźć dziewiąty wyraz ciągu arytmetycznego, jeżeli wyraz piąty i siódmy jest równy odpowiednio \(7\) i \(\sqrt{7}\).
Zadanie nr 29.
Dla jakich wartości \(x\) i \(y\) ciąg \((5, x, y, \frac{1}{5})\) jest ciągiem arytmetycznym?
Zadanie nr 31.
Pole trójkąta prostokątnego, którego długości boków tworzą ciąg arytmetyczny, wynosi 6 cm3. Znaleźć długości wszystkich boków trójkąta.
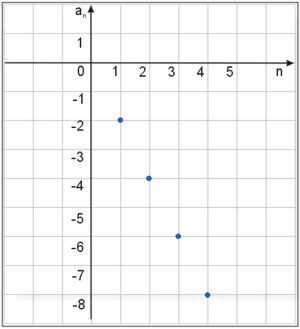
Zadanie nr 33.
Znaleźć wzór na n-ty wyraz ciągu, którego fragment wykresu został przedstawiony na ilustracji:
Zadanie nr 34.
Napisać:
a) trzy początkowe wyrazy ciągu \(a_n=\frac{n[2-(-2)^{n+1}]}{n+1}\) oraz znaleźć dziewiąty wyraz tego ciągu.
b) pięć początkowych wyrazów ciągu \(\begin{cases}a_1=2 \\ a_2=4 \\ a_n=a_{n-2}+2a_{n-1}, \ dla \ n\geq 3 \end{cases}\)
Zadanie nr 35 - maturalne.
Ciąg arytmetyczny \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\). Trzeci i piąty wyraz ciągu spełniają warunek \(a_3+a_5=58\). Wtedy czwarty wyraz tego ciągu jest równy
A. 28
B. 29
C. 33
D. 40
Zadanie nr 36 - maturalne.
Czternasty wyraz ciągu arytmetycznego jest równy \(8\), a różnica tego ciągu jest równa \((-\frac{3}{2})\). Siódmy wyraz tego ciągu jest równy:
A. \(\frac{37}{2}\)
B. \(-\frac{37}{2}\)
C. \(-\frac{5}{2}\)
D. \(\frac{5}{2}\)
Zadanie nr 37 - maturalne.
Ciąg \((x,2x+3,4x+3)\) jest geometryczny. Pierwszy wyraz tego ciągu jest równy:
A. -4
B. 1
C. 0
D. -1
Zadanie nr 38 - maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=2n^2+2n\) dla \(n\geq 1\). Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.
Zadanie nr 39 - maturalne.
Granica \(\displaystyle\lim_{n\to \infty}{\frac{(pn^2+4n)^3}{5n^6-4}}=-\frac{8}{5}\). Wynika stąd, że
A. \(p=-8\)
B. \(p=4\)
C. \(p=2\)
D. \(p=-2\)
Zadanie nr 40 - maturalne.
Dany jest ciąg geometryczny \((a_n)\) określony wzorem \(a_n=(\frac{1}{2x-371})^n\), dla \(n\geq 1\). Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą \(x\), dla której nieskończony szereg \(a_1+a_2+a_3+...\) jest zbieżny.
Zadanie nr 41 - maturalne.
W rosnącym ciągu geometrycznym \((a_n)\) , określonym dla \(n\geq 1\), spełniony jest warunek \(a_4=3a_1\). Iloraz \(q\) tego ciągu jest równy:
A. \(q=\frac{1}{3}\)
B. \(q=\frac{1}{\sqrt[3]{3}}\)
C. \(q=\sqrt[3]{3}\)
D. \(q=3\)
Zadanie nr 42 - maturalne.
W nieskończonym ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy \(a_1, a_3, a_k\) ciągu \((a_n)\), w podanej kolejności, tworzą nowy ciąg — trzywyrazowy ciąg geometryczny \((b_n)\). Oblicz \(k\).
Zadanie nr 43 - maturalne.
Oblicz granicę \(\displaystyle\lim_{n\to \infty}(\frac{11n^3+6n+5}{6n^3+1}-\frac{2n^2+2n+1}{5n^2-4})\). W poniższe kratki wpisz kolejno cyfrę jedności i pierwsze dwie cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.
Zadanie nr 44 - maturalne.
Ciąg \((b_n)\) jest określony wzorem \(b_n=3n^2-25n\) dla każdej liczby naturalnej \(n\geq 1\). Liczba niedodatnich wyrazów ciągu \((b_n)\) jest równa
A. 14
B. 13
C. 9
D. 8
Zadanie nr 45 - maturalne.
Liczby \(2,-1,-4\) są trzema początkowymi wyrazami ciągu arytmetycznego \((a_n)\), określonego dla liczb naturalnych \(n\geq 1\). Wzór ogólny tego ciągu ma postać:
A. \(a_n=-3n+5\)
B. \(a_n=n-3\)
C. \(a_n=-n+3\)
D. \(a_n=3n-5\)
Zadanie nr 46 - maturalne.
Liczby: \(x-2, 6, 12\), w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba \(x\) jest równa:
A. 0
B. 2
C. 3
D. 5
Zadanie nr 47 - maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), dane są: \(a_1=5, a_2=11\). Wtedy
A. \(a_{14}=71\)
B. \(a_{12}=71\)
C. \(a_{11}=71\)
D. \(a_{10}=71\)
Zadanie nr 48 - maturalne.
Dany jest trzywyrazowy ciąg geometryczny \((24, 6, a − 1)\). Stąd wynika, że:
A. \(\frac{5}{2}\)
B. \(\frac{2}{5}\)
C. \(\frac{3}{2}\)
D. \(\frac{2}{3}\)
Zadanie nr 49 - maturalne.
Liczby \(a, b, c\) są — odpowiednio — pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Suma tych liczb jest równa 27. Ciąg \((a−2, b, 2c+1)\) jest geometryczny. Wyznacz liczby \(a, b, c\).
Zadanie nr 50 - maturalne.
Trzywyrazowy ciąg \((15, 3x, \frac{5}{3})\) jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że:
A. \(x=\frac{3}{5}\)
B. \(x=\frac{4}{5}\)
C. \(x=1\)
D. \(x=\frac{5}{3}\)
Zadanie nr 51 - maturalne.
Dany jest ciąg \((a_n)\) jest określony wzorem \(a_n=\frac{(5-2n)}{6}\) dla \(n\geq 1\). Ciąg ten jest
A. arytmetyczny i jego różnica jest równa \(r=-\frac{1}{3}\).
B. arytmetyczny i jego różnica jest równa \(r=-2\).
C. geometryczny i jego iloraz jest równy \(q=-\frac{1}{3}\).
D. geometryczny i jego iloraz jest równy \(q=\frac{5}{6}\).
Zadanie nr 52 - maturalne.
Dla ciągu arytmetycznego \((a_n)\), określonego dla \(n\geq 1\), jest spełniony warunek \(a_4+a_5+a_6=12\). Wtedy
A. \(a_5=4\)
B. \(a_5=3\)
C. \(a_5=6\)
D. \(a_5=5\)
Zadanie nr 53 - maturalne.
Dany jest ciąg geometryczny \((a_n)\), określony dla \(n\geq 1\), w którym \(a_1=\sqrt{2}, a_2=2\sqrt{2}, a_3=4\sqrt{2}\). Wzór na n-ty wyraz tego ciągu ma postać
A. \(a_n=(\sqrt{2})^n\)
B. \(a_n=\frac{2^n}{\sqrt{2}}\)
C. \(a_n=(\frac{\sqrt{2}}{2})^n\)
D. \(a_n=\frac{(\sqrt{2})^n}{2}\)
Zadanie nr 54 - maturalne.
Dwunasty wyraz ciągu arytmetycznego \((a_n)\), określonego dla \(n\geq 1\), jest równy 30, a suma jego dwunastu początkowych wyrazów jest równa 162. Oblicz pierwszy wyraz tego ciągu.
Zadanie nr 55 - maturalne.
Liczby \(a, b, c\), spełniające warunek \(3a+b+3c=77\), są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Ciąg \((a, b+1, 2c)\) jest geometryczny. Wyznacz liczby \(a, b, c\) oraz podaj wyrazy ciągu geometrycznego.
Zadanie nr 56 - maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), dane są dwa wyrazy: \(a_1= 7 i a_8=−49\). Suma ośmiu początkowych wyrazów tego ciągu jest równa
A. -168
B. -189
C. -21
D. -42
Zadanie nr 57 - maturalne.
Dany jest ciąg geometryczny \((a_n)\), określony dla \(n\geq 1\). Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek \(\frac{a_5}{a_3}=\frac{1}{9}\). Iloraz tego ciągu jest równy:
A. \(\frac{1}{3}\)
B. \(\frac{1}{\sqrt{3}}\)
C. \(3\)
D. \(\sqrt{3}\)
Zadanie nr 58 - maturalne.
Ciąg arytmetyczny \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\). Różnicą tego ciągu jest liczba \(r=−4\), a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu: \(a_1, a_2, a_3, a_4, a_5, a_6\) jest równa 16.
a) Oblicz pierwszy wyraz tego ciągu.
b) Oblicz liczbę \(k\), dla której \(a_{k}=−78\).
Zadanie nr 59 - maturalne.
Ciąg \((a, b, c)\) jest geometryczny, ciąg \((a+1, b+5, c)\) jest malejącym ciągiem arytmetycznym oraz \(a+b+c=39\). Oblicz \(a, b, c\).
Zadanie nr 60 - maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=2n^2\) dla \(n\geq 1\). Różnica \(a_5-a_4\) jest równa
A. \(4\)
B. \(20\)
C. \(36\)
D. \(18\)
Zadanie nr 61 - maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla \(n\geq 1\), czwarty wyraz jest równy 3, a różnica tego ciągu jest równa 5. Suma \(a_1+a_2+a_3+a_4\) jest równa
A. \(-42\)
B. \(-36\)
C. \(-18\)
D. \(6\)
Zadanie nr 62 - maturalne.
Wszystkie wyrazy ciągu geometrycznego \((a_n)\), określonego dla \(n\geq 1\), są dodatnie. Wyrazy tego ciągu spełniają warunek \(6a_1-5a_2+a_3= 0\). Oblicz iloraz \(q\) tego ciągu należący do przedziału \(\langle 2\sqrt{2}, 3\sqrt{2}\rangle\).
Zadanie nr 63 - maturalne.
Ciąg \((a_n)\) jest określony wzorem \(\frac{3n^2+7n-5}{11-5n+5n^2}\) dla każdej liczby naturalnej \(n\geq 1\). Granica tego ciągu jest równa
A. \(3\).
B. \(\frac{1}{5}\).
C. \(\frac{3}{5}\).
D. \(-\frac{5}{11}\).
Zadanie nr 64 - maturalne.
W trzywyrazowym ciągu geometrycznym \((a_1, a_2, a_3)\) spełniona jest równość \(a_1+a_2+a_3=\frac{21}{4}\). Wyrazy \(a_1, a_2, a_3\) są — odpowiednio — czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz \(a_1\).
Zadanie nr 65 - maturalne.
Oblicz granicę
.
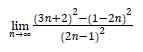W poniższe kratki wpisz kolejno – od lewej do prawej – cyfrę jedności i pierwsze dwie cyfry po
przecinku skończonego rozwinięcia dziesiętnego otrzymanego wyniku.
Zadanie nr 66 - maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=\frac{2n^2-30n}{n}\) dla każdej liczby naturalnej \(n\geq 1\). Wtedy \(a_7\) jest równy
A. (-196)
B. (-32)
C. (-26)
D. (-16)
Zadanie nr 67 - maturalne.
W ciągu arytmetycznym \((a_n)\), określonym dla każdej liczby naturalnej \(n\geq 1\), \(a_5=-31\) oraz \(a_{10}=−66\). Różnica tego ciągu jest równa
A. (-7)
B. (-19,4)
C. 7
D. 19,4
Zadanie nr 68 - maturalne.
Wszystkie wyrazy nieskończonego ciągu geometrycznego \((a_n)\), określonego dla każdej liczby naturalnej \(n\geq 1\), są dodatnie i \(9a_5=4a_3\). Wtedy iloraz tego ciągu jest równy
A. \(\frac{2}{3}\)
B. \(\frac{3}{2}\)
C. \(\frac{2}{9}\)
D. \(\frac{9}{2}\)
Zadanie nr 69 - maturalne.
W ciągu arytmetycznym \(a_n\), określonym dla każdej liczby naturalnej \(n\geq 1\), \(a_1=-1\) i \(a_4=8\). Oblicz sumę stu początkowych kolejnych wyrazów tego ciągu.
Zadanie nr 70 - maturalne.
Ciąg \((a_n)\) jest określony dla każdej liczby naturalnej \(n\geq 1\) wzorem \(a_n=\frac{(7p-1)n^3+5pn-3}{(p+1)n^3+n^2+p}\), gdzie \(p\) jest liczbą rzeczywistą dodatnią. Oblicz wartość \(p\), dla której granica ciągu \(a_n\) jest równa \(\frac{4}{3}\). W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.
Zadanie nr 71 - maturalne.
Ciąg \((a_n)\) jest określony wzorem \(a_n=2^n\cdot (n+1)\) dla każdej liczby naturalnej \(n\geq 1\). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Wyraz \(a_4\) jest równy
A. 64
B. 40
C. 48
D. 80
Zadanie nr 72 - maturalne.
Trzywyrazowy ciąg \((27,9,a-1)\) jest geometryczny. Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba \(a\) jest równa
A. 3
B. 0
C. 4
D. 2
Zadanie nr 73 - maturalne.
Pan Stanisław spłacił pożyczkę w wysokości 8910 zł w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 30 zł. Oblicz kwotę pierwszej raty. Zapisz obliczenia.
Zadanie nr 74 - maturalne.
W chwili początkowej (\(t=0\)) masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 19% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej \(t\geq 0\) funkcja \(m(t)\) określa masę substancji w gramach po \(t\) pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji \(m(t)\). Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od \(1,5\) grama. Zapisz obliczenia.
Zadanie nr 75 - maturalne.
Określamy kwadraty \(K_1, K_2, K_3, ...\) następująco:
• \(K_1\) jest kwadratem o boku długości \(a\).
• \(K_2\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_1\) i dzieli ten bok w stosunku \(1:3\).
• \(K_3\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_2\) i dzieli ten bok w stosunku \(1:3\).
i ogólnie, dla każdej liczby naturalnej \(n\geq 2\)
• \(K_n\) jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu \(K_n-1\) i dzieli ten bok w stosunku \(1:3\).
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
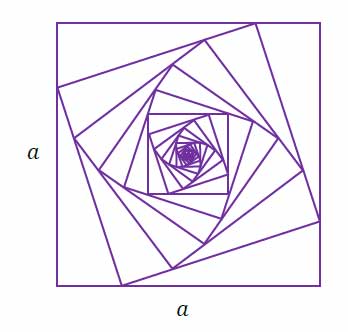
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu. Zapisz obliczenia.
Liczba odnalezionych zadań w zbiorze: 75.
Oznaczenia
Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom rozszerzony.
