Zadania — pochodna funkcji
Znajdziesz tutaj zadania z pochodnej funkcji (rachunek różniczkowy). Przykładowymi zadaniami opatrzono takie tamaty jak własności pochodnej, pochodna funkcji złożonej, czy zwykłe obliczanie pochodnych. To zadania z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
Zadanie nr 1.
Obliczyć pochodną funkcji \(f(x)=-x^2+x-1\) w punkcie \(x_0=-1\).
Zadanie nr 3.
Obliczyć pochodną funkcji \(f(x)=\frac{1}{x+1}\) w punkcie \(x_0=0\).
Zadanie nr 5.
Obliczyć pochodną funkcji \(f(x)=\begin{cases} x^2 \ dla \ x\geq 0 \\ -2x^2 \ dla \ x<0 \end{cases}\) w punkcie \(x_0=0\).
Zadanie nr 6.
Obliczyć pochodną funkcji
\(a) f(x)=-\frac{1}{2}\)
\(b) g(x)=x^{17}\)
\(c) h(x)=x^{\frac{1}{3}}\)
\( d) i(x)=x\)
\( e) j(x)=\sqrt{2}\)
Zadanie nr 7.
Obliczyć pochodną funkcji:
\(a) f(x)=-x+5\)
\(b) g(x)=-5x^2+2\sqrt{x}\)
\( c) h(x)=\sin{x}+2\cos{x}\)
\( d) i(x)=-\frac{1}{x}-tgx\)
\( e) j(x)=3x^3-2x^2+x-1\)
Zadanie nr 8.
Obliczyć pochodną funkcji:
\(a) f(x)=x\sin{x}\)
\(b) g(x)=\sin^2{x}\)
\(c) h(x)=x\sqrt{x}\)
Zadanie nr 9.
Obliczyć pochodną funkcji:
a) \(f(x)=\frac{\sin{x}}{x}\)
b) \(f(x)=\frac{2x+1}{3x-1}\)
c) \(f(x)=\frac{\sin{x}}{\cos{x}}\)
Zadanie nr 10.
Obliczyć pochodną funkcji:
a) \(f(x)=\frac{\sqrt{x}}{x}\)
b) \(f(x)=\frac{5x^3-x+1}{x^2-1}\)
c) \(f(x)=\frac{5x^4-3x^2}{2x^3-1}\)
Zadanie nr 11.
Obliczyć pochodną funkcji \(f(x)=\frac{\sqrt[5]{x}}{10x^8}\).
Zadanie nr 12.
Obliczyć pochodną funkcji:
a) \(f(x)=\sin{2x}\)
b) \(f(x)=\sqrt{x^3-2x+1}\)
c) \(f(x)=\sqrt[3]{1+x^2}\)
Zadanie nr 13.
Obliczyć pochodną funkcji:
a) \(f(x)=\sin{(\cos{x})}\)
b) \(f(x)=\sqrt{x^2+\sqrt{x}}\)
Zadanie nr 14.
Obliczyć pochodną funkcji \(f(x)=\sin^2{x}\cdot \cos^2{x}\).
Zadanie nr 15.
Obliczyć pochodną funkcji \(f(x)=\frac{\sin{2x}}{1+cos^2{x}}\).
Zadanie nr 16.
Obliczyć drugą pochodną funkcji:
a) \(f(x)=\sqrt{x}\)
b) \(f(x)=x^2-x^3+\frac{1}{x^3}\)
Zadanie nr 17.
Obliczyć drugą pochodną funkcji:
a) \(f(x)=\cos^2{2x}\)
b) \(f(x)=\frac{x^2+1}{x^2-1}\)
Zadanie nr 18.
Dla jakiej wartości argumentu \(x\) druga pochodna funkcji \(f(x)=\frac{1}{1+x}\) jest równa \(\frac{1}{4}\)?
Zadanie nr 20.
Znaleźć równanie stycznej do krzywej \(f(x)=\frac{2}{x}\) w punkcie \((2,1)\).
Zadanie nr 21.
Znaleźć równanie stycznej do krzywej \(f(x)=\sin{x}\) w punkcie \((\frac{\pi}{2},1)\).
Zadanie nr 22.
Znaleźć równanie stycznej do okręgu \((x-1)^2+y^2=2\) w punkcie \((1,-\sqrt{2})\).
Zadanie nr 23.
Wyznaczyć przedziały monotoniczności funkcji \(f(x)=\frac{x^2}{x-1}\).
Zadanie nr 24.
Wyznaczyć przedziały monotoniczności funkcji \(f(x)=x^3-6x+5\).
Zadanie nr 25.
Wyznaczyć przedziały monotoniczności funkcji \(f(x)=x^2+\frac{2}{x}\).
Zadanie nr 26.
Wyznaczyć przedziały monotoniczności funkcji \(f(x)=\sqrt{2}+1\).
Zadanie nr 31.
Znaleźć największą i najmniejszą wartość funkcji \(f(x)=3x+\frac{1}{x}\) w przedziale \(\langle-1;1\rangle\).
Zadanie nr 32.
Znaleźć największą i najmniejszą wartość funkcji \(f(x)=1+\frac{x^2}{x+2}\) w przedziale \(\langle -\frac{3}{2};0\rangle\).
Zadanie nr 35.
Rzucony kamień zakreśla w powietrzu tor opisany równaniem \(y=x-x^2\). Jakie jest maksymalne wzniesienia kamienia?
Zadanie nr 36.
Jakie wymiary powinna mieć metalowa puszka w kształcie walca, aby przy określonej pojemności \(V\) zużyć możliwie najmniej blachy do jej wykonania?
Zadanie nr 37.
Zbadać przebieg zmienności funkcji \(f(x)=x^3+x^2-5x+3\) i naszkicować jej wykres.
Zadanie nr 38.
Zbadać przebieg zmienności funkcji \(f(x)=\frac{x^2-1}{x-4}\) i naszkicować jej wykres.
Zadanie nr 39.
Zbadać przebieg zmienności funkcji \(f(x)=\frac{4x+1}{2x^2-4x}\) i naszkicować jej wykres.
Zadanie nr 40.
Zbadać przebieg zmienności funkcji \(f(x)=\frac{x^3+1}{x^2}\) i naszkicować jej wykres.

Zadanie nr 41 - maturalne.
Funkcja \(f(x)=\frac{3x-1}{x^2+4}\) jest określona dla każdej liczby rzeczywistej \(x\). Pochodna tej funkcji jest określona wzorem:
A. \(f'(x)=\frac{-3x^2+2x+12}{(x^2+4)^2}\)
B. \(f'(x)=\frac{-9x^2+2x-12}{(x^2+4)^2}\)
C. \(f'(x)=\frac{3x^2-2x-12}{(x^2+4)^2}\)
D. \(f'(x)=\frac{9x^2-2x+12}{(x^2+4)^2}\)

Zadanie nr 42 - maturalne.
Parabola o równaniu \(y=2-\frac{1}{2}x^2\) przecina oś \(Ox\) układu współrzędnych w punktach \(A=(- 2,0)\) i \(B=(2,0)\). Rozpatrujemy wszystkie trapezy równoramienne \(ABCD\), których dłuższą podstawą jest odcinek \(AB\), a końce \(C\) i \(D\) krótszej podstawy leżą na paraboli (zobacz rysunek).
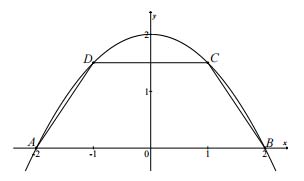
Wyznacz pole trapezu \(ABCD\) w zależności od pierwszej współrzędnej wierzchołka \(C\). Oblicz współrzędne wierzchołka \(C\) tego z rozpatrywanych trapezów, którego pole jest największe.

Zadanie nr 43 - maturalne.
Funkcja \(f\) określona jest wzorem \(f(x)=x^3-2x^2+1\) dla każdej liczby rzeczywistej \(x\). Wyznacz równania tych stycznych do wykresu funkcji \(f\), które są równoległe do prostej o równaniu \(y=4x\).

Zadanie nr 44 - maturalne.
Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

Zadanie nr 45 - maturalne.
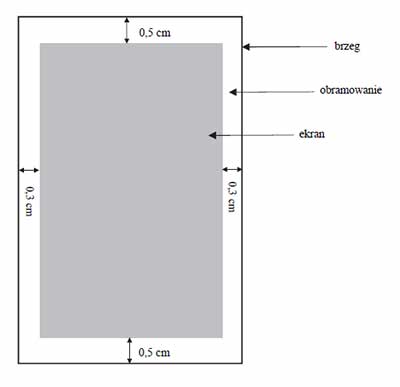
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe 0,5 cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe 0,3 cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię 60 cm2. Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.

Zadanie nr 46 - maturalne.
Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 144 m3. Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów.
Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 1 m2 dna
– 75 zł za 1 m2 ściany bocznej.
Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.

Zadanie nr 47 - maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{x^3-8}{x-2}\) dla każdej liczby rzeczywistej \(x\neq 2\). Wartość pochodnej tej funkcji dla argumentu \(x=\frac{1}{2}\) jest równa
A. \(\frac{3}{4}\)
B. \(\frac{9}{4}\)
C. 3
D. \(\frac{54}{8}\)

Zadanie nr 48 - maturalne.
Rozpatrujemy wszystkie trójkąty równoramienne o obwodzie równym 18.
a) Wykaż, że pole \(P\) każdego z tych trójkątów, jako funkcja długości \(b\) ramienia, wyraża się wzorem \(P(b)=\frac{(18-2b)\cdot \sqrt{18b-81}}{2}\).
b) Wyznacz dziedzinę funkcji \(P)\.
c) Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole.

Zadanie nr 49 - maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=\frac{3x^2-2x}{x^2+2x+8}\) dla każdej liczby rzeczywistej \(x\). Punkt \(P=(x_0,3)\) należy do wykresu funkcji \(f\). Oblicz \(x_0\) oraz wyznacz równanie stycznej do wykresu funkcji \(f\) w punkcie \(P\). Zapisz obliczenia.

Zadanie nr 50 - maturalne.
Funkcja \(f\) jest określona wzorem \(f(x)=81^{\log_3{x}}+\frac{2\cdot\log_2 {\sqrt{7}}\cdot \log_3{2}}{3}\cdot x^2-6x\) dla każdej liczby dodatniej \(x\).
1. Wykaż, że dla każdej liczby dodatniej \(x\) wyrażenie \(81^{\log_3{x}}+\frac{2\cdot\log_2 {\sqrt{7}}\cdot \log_3{2}}{3}\cdot x^2-6x\) można równoważnie przekształcić do postaci \(x^4+x^2-6x\).
2. Oblicz najmniejszą wartość funkcji \(f\) określonej dla każdej liczby dodatniej \(x\). Zapisz obliczenia. Wskazówka: przyjmij, że wzór funkcji \(f\) można przedstawić w postaci \(f(x)=x^4+x^2-6x\).
Liczba odnalezionych zadań w zbiorze: 50.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.